Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2013 11:35
Limita ln
Zdravím, potřebovala bych poradit, jak se dělá limita pro x->
pro 
..
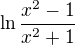hlavně tedy nevím, jak naložit s tím ln. Jinak bych asi zlomek upravila podle L'Hospitalova pravidla..
předem moc děkuji za odpověď :-)
Offline
- (téma jako vyřešené označil(a) jelena)
#2 19. 01. 2013 11:49
?#3 19. 01. 2013 11:55
Re: Limita ln
↑ standyk:
nechápu otázku :(..
to za logaritmem je nekonecno lomene nekonecnem, po uziti L'HP mi vyjde, ze je to ln1, takže výsledek by měl být nula.. otázkou je, jestli je takové řešení "legální" :D
Offline
#4 19. 01. 2013 12:00
Re: Limita ln
↑ monttyna:
Myslím to tak, že k čomu sa blíži 
. Keďže ide o limitu v nekonečne tak v tomto prípade stačí porovnať koeficienty pri najvyšších mocninách (keďže čitateľ aj menovateľ majú rovnakú najvyššiu mocninu). Zvyšná úvaha je správna (argument ide k 1 tak logaritmus pôjde k 0).
Offline