Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Gaussova rovina-kružnice s hezkým řešením (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 01. 2013 16:30
Gaussova rovina-kružnice s hezkým řešením
Dobrý den,
mám zadání: Nalezněte 2 kružnice, které procházejí postupně body 8+10i a 4+12i, poloměry kružnic jsou různé, a kružnice mají právě 2 průsečíky. Nalezněte hezké řešení.
Zkoušela jsem to řešit tak, že jsem si zvolila treba S1=0+0i, nebo že jsem si zvolila pěkný poloměr, ale vždy mi potom vychází nepěkné řešení druhé kružnice, zkoušela jsem mnoho čísel ale nikdy mi to nevyšlo.
Mohl by mi prosím někdo poradit, jak si mám zvolit ty 2 kružnice aby mi vyšly "hezká" čísla? děkuji předem
Offline
- (téma jako vyřešené označil(a) simcilka)
#2 20. 01. 2013 23:09 — Editoval Brano (20. 01. 2013 23:34)
Re: Gaussova rovina-kružnice s hezkým řešením
Vsetky kruznice prechadzajuce bodmi 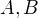 budu mat stred na osi usecky
budu mat stred na osi usecky  . Takze najprv si mozme najst tuto os. Prechadza bodom
. Takze najprv si mozme najst tuto os. Prechadza bodom  . Normalovy vektor ma
. Normalovy vektor ma 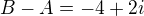 , teda smerovy vektor je
, teda smerovy vektor je  (resp.
(resp.  ). Cize parametricke vyjadrenie tej osi je
). Cize parametricke vyjadrenie tej osi je  kde
kde 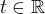 - pricom pre celociselne
- pricom pre celociselne  su tie stredy "pekne". Ak si vyberieme konkretny stred (prisluchajuci t) tak polomer bude
su tie stredy "pekne". Ak si vyberieme konkretny stred (prisluchajuci t) tak polomer bude 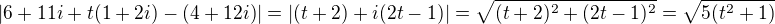 .
.
Teraz tak od pohladu mozme zvolit 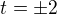 a v oboch pripadoch dostaneme polomer
a v oboch pripadoch dostaneme polomer 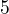 a stredy budu
a stredy budu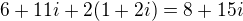 a
a 
a teda tie kruznice su a
a 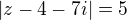 .
.
Su dost pekne? :-)
edit: Sem
http://forum.matweb.cz/viewtopic.php?id=55734
som zadal otazku, ktora sa tyka najdenia inych peknych kruznic (ja zatial ine neviem) tak mozes sledovat ci to niekto iny vyriesi.
Offline
#3 21. 01. 2013 00:30
Re: Gaussova rovina-kružnice s hezkým řešením
děkuji to je dosta pekné řešení, ale kružnice měly mít různé poloměry a sice to zadani není přesne dané ale pochopila jsem to tak, že 1 kružnice procházá jedním bodem a druha druhym bodem.
a já jsem to právě tak řešila, že každá kružnice prochází jedním bodem. Tvoje řešení bych jinak vedela, děkuji, a nevís jak to řesit ted?
Offline
#4 21. 01. 2013 00:46
Re: Gaussova rovina-kružnice s hezkým řešením
Aha tie rozne polomery som si tam nevsimol a to s tymi bodmi som teda asi zle pochopil. Ale co je na tom potom tazke mozes si zvolit takmer lubovolne dva body ako stredy tych kruznic - staci aby sa niekde pretali (nedotkli), ci aj tie prieniky maju byt "pekne" (s celociselnymi koeficientami)?
Offline
#5 21. 01. 2013 01:15
Re: Gaussova rovina-kružnice s hezkým řešením
Nuz ale aj tomuto "novemu" zadaniu by zodpovedalo moje riesenie ak by sa nasla kruznica s inym polomerom, nie? Lebo jedna prechadza jednym bodom a druha druhym, len "akoze nahodou" aj prva druhym a druha prvym cize je zabezpecene, ze sa pretnu v celociselnych bodoch. Tak mozes zobrat 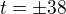 potom vyjde
potom vyjde 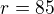 .
.
Vysledok vdaka W|A
http://www.wolframalpha.com/input/?i=so … r+integers
dosadil som 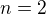 .
.
Offline
#6 21. 01. 2013 08:55
Re: Gaussova rovina-kružnice s hezkým řešením
co jsem pochopila ze zadnani tak i pruniky maji byt hezke-cca celocislene nebo nejaky zlomek, 1/2,..ja jsem si prave ze zvolila uz asai 10 moznosti a nikdy mi to nevyslo pekne, ukol ma byt v tom jak vymyslet v podstate zadani aby to zakum vychazelo,..
omlouvam se ale tomu druhemu prispevku nerozumim:(
Offline
#8 21. 01. 2013 14:58
Re: Gaussova rovina-kružnice s hezkým řešením
Děkuji už to vidím, teď to jen musím vyřešit pomoci komplexníxh čísel, mám zakázano používat euklidovské postupy. Ale děkuji pomohl jsi mi vubec me to nenapadlo si to nejdriv vyresit analyticky a pak az v gaussove rovine,..
Offline
#9 21. 01. 2013 15:27
Re: Gaussova rovina-kružnice s hezkým řešením
↑ simcilka:
Postup je samozrejme prebraty z analytickej geometrie, ale podla mna tak ako som to zapisal to je legalny postup vyuzivajuci (iba) Gaussovu rovinu. Ale isteze, prepis si to tak ako to tebe, alebo tvojim ziakom bude najviac vyhovovat :-).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Gaussova rovina-kružnice s hezkým řešením (TOTO TÉMA JE VYŘEŠENÉ)

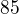 . T.j. mozes zobrat napr.
. T.j. mozes zobrat napr.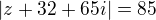

 , druha prechadza
, druha prechadza  .
.