Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matematická indukce pro uzavřený tvar sumy (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 01. 2013 23:04
- OrangeTree
- Příspěvky: 61
- Reputace: 0
Matematická indukce pro uzavřený tvar sumy
Ahoj :).
Ze zadané sumy 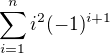 se mi podařilo odvodit uzavřený tvar
se mi podařilo odvodit uzavřený tvar 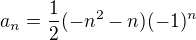 .
.
Svůj výsledek mám potvrdit matematickou indukcí, což je pro mě vždy kámen úrazu.
Poraďte mi prosím, co je první krok? Dokazuji 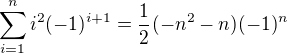 . Kterou stranu rovnice mám použít na přechod
. Kterou stranu rovnice mám použít na přechod 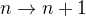 ?
?
Offline
- (téma jako vyřešené označil(a) OrangeTree)
#2 21. 01. 2013 23:21 — Editoval standyk (21. 01. 2013 23:26)
Re: Matematická indukce pro uzavřený tvar sumy
↑ OrangeTree:
Ahoj,
V prvom kroku dokážeš, že to platí pre n = 1.
V druhom kroku si vezmeš svoj vzťah ako indukčný predpoklad a budeš dokazovať že:
A celý problém indukcie je teraz nájsť čo bude namiesto tých bodiek, resp. ako sa dopracovať pomocou úprav k tomu výrazu napravo.
Offline
#3 22. 01. 2013 10:18
- OrangeTree
- Příspěvky: 61
- Reputace: 0
Re: Matematická indukce pro uzavřený tvar sumy
↑ standyk:
Děkuju za názornou ukázku, už tomu rozumím :).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matematická indukce pro uzavřený tvar sumy (TOTO TÉMA JE VYŘEŠENÉ)
