Matematické Fórum

Zlatohlavok · 22. 01. 2013 20:44

Môžete mi prosim vás povedať prečo,
pre danú funkciu f:<0,3>->R , f(x)=|x-1| neplatí Lagrangeova veta.

Jej znenie je:
Nech je daná funkcia f:<a,b>->R
Nech je funkcia f spojitá na intervale <a,b>
Nech je funkcia f diferencovatelna na intervale (a,b)

Potom existuje c € (a,b) take, ze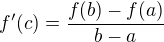

$f'(c)=\frac{f(b)-f(a)}{b-a}$

ďakujem :)

LukasM · 22. 01. 2013 20:50

↑ Zlatohlavok:
Lagrangeova věta samozřejmě platí. Ale protože pro tvůj případ není splněn předpoklad (3), neplatí její tvrzení.

Zlatohlavok · 22. 01. 2013 20:59

Aha, cize f'(c) = f(0)-f(3) / 0-3 = -1 - 2 / -3 = 1

1 patrí do intervali <0,3>

Tak kde je problém? Či som sa pomýlil niekde?

Diky

LukasM · 22. 01. 2013 21:07

↑ Zlatohlavok:
Naprosto nechápu o čem mluvíš. Ale ani trochu. Máš teda špatně i to dosazení, protože jsi přehodil a a b, ale to tvůj problém nevyřeší.

Každopádně jeden z předpokladů věty je "Nech je funkcia f diferencovatelna na intervale (a,b)" a ten pro tvou funkci a tvůj interval není splněn.

Zlatohlavok · 22. 01. 2013 21:56

Pomýlil som sa.
Malo by to byť teda
$\frac{0-2}{1-1} = \infty$ => nepadrí do intervalu (-1,1)

Takto je to myslené? Ďakujem

Brano · 22. 01. 2013 22:03

Skusal si aj precitat to co ti ↑ LukasM: napisal?

Zlatohlavok · 23. 01. 2013 09:40

Áno, samozrejme čítal som to.
Veď diverencovatelnosť sa počíta podla vzorca 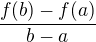$\frac{f(b)-f(a)}{b-a}$ tak som dosadil hranice do menovatela a do čitatela som dosadil f(a), f(b) funkcie f=|x-1|

LukasM · 23. 01. 2013 10:03 — Editoval LukasM (23. 01. 2013 10:14)

↑ Zlatohlavok:
Diferencovatelnost se podle žádného takového vzorce nepočítá. Funkce je na intervalu diferencovatelná, pokud v každém bodě toho intervalu má konečnou derivaci. Tvá funkce v bodě 1 nemá derivaci, takže na žádném intervalu který obsahuje bod 1 není diferencovatelná.

Derivace v bodě a je definována jako $\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$ . Tato limita v bodě 1 neexistuje.

Edit: oprava ve vzorci pro derivaci, přehnal jsem to s kopírováním

Brano · 23. 01. 2013 10:03

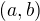Aha tak uz zacinam tusit. Nie diferencovatelnost na $(a,b)$ znamena, ze pre lubovolne 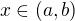$x\in (a,b)$ existuje limita $\lim_{y\to x}\frac{f(y)-f(x)}{y-x}$ - urcite sa v tom podiele nestaci pozerat na koncove body. Diferencovatelnost zlyha konkretne v $x=1$ .