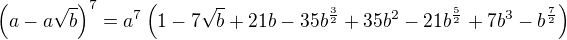Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 26. 01. 2013 13:49
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Upravení vzorce na 7mou
Offline
#5 26. 01. 2013 14:10 — Editoval Blackflower (26. 01. 2013 14:11)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Offline
#7 26. 01. 2013 14:18
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Upravení vzorce na 7mou
↑ ihnaja: Skús si pozrieť ten odkaz, čo som sem dala pár príspevkov dozadu, je tam všeobecná binomická veta, plus si pozri môj náznak riešenia a skús sa s tým pohrať. Potom sem napíš svoj postup a skontrolujeme.
Offline
#11 27. 01. 2013 12:56 — Editoval Blackflower (27. 01. 2013 12:58)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Upravení vzorce na 7mou
↑ ihnaja: Treba stále skúšať, aj keď to spočiatku nejde, lebo tým, že ti to sem niekto napíše celé, sa to nenaučíš... teraz, keď sem už kolega ↑ jarrro: napísal výsledok, skús si to rozpísať podľa vzorca uvedeného vyššie (binomická veta - to so sumou) pre každé k (myslím, že jarrro tam má drobný preklep, v exponentoch pri a,b má byť písmeno k namiesto i).
Ak sa nedostaneš k správnemu výsledku, napíš sem celý svoj postup, vždy sa nám lepšie spolupracuje, keď vidíme, k čomu sa človek dostal...
Offline
#12 27. 01. 2013 13:03
Re: Upravení vzorce na 7mou
↑ Blackflower:dík opravené pôvodne som tam totiž mal sčítací index i, ale potom som si uvedomil, že dosť splýva so znakom faktoriálu (výkričník)
MATH IS THE BEST!!!
Offline
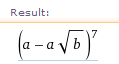

 (pred zátvorkou teda bude
(pred zátvorkou teda bude 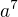 ) a na zátvorku použiť binomickú vetu:
) a na zátvorku použiť binomickú vetu: ![kopírovat do textarea $(a-a\sqrt{b})^7=a^7(1-\sqrt{b})=a^7[{7 \choose 0}1^7\sqrt{b}^0-{7 \choose 1}1^6\sqrt{b}^1+...]$](/mathtex/7d/7db1629423c1cc8a09cec5706d532ffd.gif)