Matematické Fórum

Zeck · 31. 01. 2013 05:12

$f(t)=|t|$ - párna funkcia
$-1<t<1$
$T=2$
$l=1$

$a_{0}=1$
$a_{k}=\frac{2}{k^{2}{\pi}^2 }.(\cos k\pi -1)=\frac{2}{k^{2}{\pi}^2 }.((-1)^{k}-1)$
$f(t)\sim \frac{1}{2}+\sum_{k=1}^{\infty }\frac{-4}{(2k-1)^2\pi ^2}.cos (2k-1)\pi t$

Mám 2 otázky:
1. ako vzniklo z $(\cos k\pi -1)$ toto $((-1)^{k}-1)$
2.prečo je vo výsledku za sumou $\frac{-4}{(2k-1)^2\pi ^2}$ Odkiaľ to je?
Dakujem.

jelena · 31. 01. 2013 11:35

Zdravím,

z $(\cos k\pi -1)$ vznikne $((-1)^{k}-1)$ když budeš dosazovat za k přirozená (ale také i celá) čísla, potom odvodíš tento zjednodušený zápis,
$\frac{-4}{(2k-1)^2\pi ^2}$ vznikne při dosazovaní lichých hodnot k (pro sudé hodnoty se tento člen vynuluje) - podrobně je zde, příklad 8.1.1 b). Potom je všechno dáne do vzorce. Stačí tak? Děkuji.

Zeck · 31. 01. 2013 19:07

↑ jelena:

a ako vznikne vo vysledku argument kosinu $(2k-1)$ ?

jelena · 31. 01. 2013 22:29 — Editoval jelena (01. 02. 2013 00:07)

↑ Zeck:

ve vyjádření $a_n$ po integrování a dosazení mezí jsi měl dojit k momentu $a_{n}=\frac{2}{n^{2}{\pi}^2 }\cdot\left[ \cos(\pi nt)\right]^1_0=\frac{2}{n^{2}{\pi}^2 }\cdot$\cos(\pi n\cdot 1)-\cos 0$$

edit: odstranila jsem 2 v cos(2pint) - byl to překlep.

A od tohoto momentu rozebereš 2 situace:

pokud je n sude a zapíšeme jako 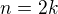$n=2k$
pokud je n liché a zapíšeme jako $n=2k-1$

Je to tak vidět a jak dopadne? Děkuji.

Zeck · 05. 02. 2013 12:48

Dakujem pekne, velmi mi to pomohlo! :)

Matematické Fórum

#1 31. 01. 2013 05:12

Fourierov rad

#2 31. 01. 2013 11:35

Re: Fourierov rad

#3 31. 01. 2013 19:07

Re: Fourierov rad

#4 31. 01. 2013 22:29 — Editoval jelena (01. 02. 2013 00:07)

Re: Fourierov rad

#5 05. 02. 2013 12:48

Re: Fourierov rad

Zápatí