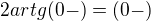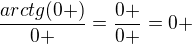Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nespojitost v bodě x=0 (TOTO TÉMA JE VYŘEŠENÉ)
#3 05. 02. 2013 15:44
Re: Nespojitost v bodě x=0
↑ honyik:
bod nespojitosti 1. druhu = nerovnaji se ti limity z obou stran ale existuji, kdyz budes pocitat tu limitu zprava tak zlhospitalujes a vyjde ti 1 zleva 0
↑ honyik:
u bodu odstranitelne nespojitosti chces, aby se ti limity z obou stran rovnaly
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#4 05. 02. 2013 15:53
Re: Nespojitost v bodě x=0
No ale u toho druhého vychází horní funkce 1 a dolní 0. Nebo všechno, co je  mám zlHospitalizovat?
mám zlHospitalizovat?
Protože, jsme myslím, že brali první spojistosti, před tím vlastně limity, až potom derivace, tak jestli třeba náhodou nějaká jiná metoda? (jen otázka jestli něco takového existuje)
Děkuji za pomoc! :)
Offline
#5 05. 02. 2013 16:57
Re: Nespojitost v bodě x=0
↑ honyik:Problem je v tom, ze 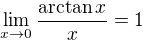 . Nezabudaj, ze obrazok
. Nezabudaj, ze obrazok  nepredstavuje ziadne realne cislo a limita podobnych vyrazov moze byt akakolvek, alebo vobec nemusi existovat. Osobne by som radil uplne sa vyhnut pisaniu niecoho takeho ako
nepredstavuje ziadne realne cislo a limita podobnych vyrazov moze byt akakolvek, alebo vobec nemusi existovat. Osobne by som radil uplne sa vyhnut pisaniu niecoho takeho ako  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nespojitost v bodě x=0 (TOTO TÉMA JE VYŘEŠENÉ)