Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 05. 02. 2013 17:27
Re: limitaa
↑ Rumburak: dakujem ale uzivatel brano mi pomohol
vedeli by ste mi pomoct aj s tymto problemom? 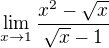
Offline
#17 05. 02. 2013 20:42
Re: limitaa
↑ Kittie:
... nebo, pokud nic nevíš a l'Hospitalovat nesmíš, to rozbiješ součtovými vzorci na něco, kde se bude vyskytovat pouze  a cosiny (které ti nevadí, protože mají v nule limitu 1). Pak pokrátíš co nejvíc sinů a uvidíš.
a cosiny (které ti nevadí, protože mají v nule limitu 1). Pak pokrátíš co nejvíc sinů a uvidíš.  .
.
Všechny ty cosiny samozřejmě můžeš zahazovat už ve chvíli, kdy se objeví (já je tam nechával jen pro přehlednost a protože ctrl+c ctrl+v je snadné), takže to ani není nijak složitá úprava.
Offline

![kopírovat do textarea $\lim_{x\to0}\frac{\sqrt[3]{1+x^{2}}-1}{x^{2}}$](/mathtex/14/14005dc880f6a155343558a04db6cf41.gif)
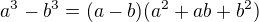 T.j. vynasob citatela aj menovatela vyrazom
T.j. vynasob citatela aj menovatela vyrazom ![kopírovat do textarea $\left(\sqrt[3]{1+x^{2}}\right)^2+\sqrt[3]{1+x^{2}}+1$](/mathtex/b3/b3a51e73ea5a2415a58a4d7fcc2ce676.gif) .
. dostáváme
dostáváme ![kopírovat do textarea $\lim_{x\to0}\frac{\sqrt[3]{1+x^{2}}-1}{x^{2}} = \lim_{h\to0+}\frac{\sqrt[3]{1+h}-1}{h} = \lim_{h\to0+}\frac{\sqrt[3]{1+h}-\sqrt[3]{1}}{h}$](/mathtex/92/92b37d649b028c1c1f718e3cafc9a217.gif) ,
,  v bodě
v bodě 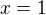 (viz definice derivace).
(viz definice derivace). ? alebo substituciu? aj tak mi to nejako nevychádza
? alebo substituciu? aj tak mi to nejako nevychádza

 x
x  =
= 
 ?
?