Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 02. 2013 06:53
Re: Porovnávání itegrálů
↑ honyik:Navrhujem upravit nerovnost tak, aby na pravej strane bola nula. Potom vyuzit aditivnost integralu, cize dat obe funkcie vlavo pod spolocny integral. No a potom si predstavit graf funkcii pod integralom vlavo. Z neho uz nie je tazke uvidiet, kedy je 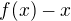 nezaporna.
nezaporna.
Offline
#3 06. 02. 2013 12:28
Re: Porovnávání itegrálů
↑ vlado_bb:
Jasný, díky moc.
Mohl bych se zeptat, jak to bude tady?
Graf by měl vypadat nějak takhle, přeci na tom intervalu je kladný.
Děkuji za pomoc! :)
Offline
#4 06. 02. 2013 17:10
Re: Porovnávání itegrálů
↑ honyik:Netrap sa s grafom funkcie ![kopírovat do textarea $x-\sqrt[3]{x}$](/mathtex/8d/8d4bb45a6523010b990f8d3c7e136a09.gif) , radsej si do toho isteho obrazku nakresli
, radsej si do toho isteho obrazku nakresli  a k nej funkciu, ktora ta zaujima, teda napriklad aj ta tretia odmocnina. Potom uvidis, ktora je na danom intervale vacsia a ktora mensia.
a k nej funkciu, ktora ta zaujima, teda napriklad aj ta tretia odmocnina. Potom uvidis, ktora je na danom intervale vacsia a ktora mensia.
Offline