Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 08. 02. 2013 20:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: binomická věta
↑ ihnaja:
Zdravím,
pokud je vzorec 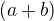 a je potíž s jeho použitím v případě
a je potíž s jeho použitím v případě  , potom lze přepsat
, potom lze přepsat  , tedy ve Tvém případě použití binomické věty zřejmě se zarazilo na přepisu
, tedy ve Tvém případě použití binomické věty zřejmě se zarazilo na přepisu  a dále všude používat včetně nových závorek.
a dále všude používat včetně nových závorek.
Pravý účel příspěvku - označ, prosím, témata, co jsi založil za vyřešená, pokud tomu tak je. Děkuji.
Offline
 aaa jedu tímto způsobem 6 nad 0
aaa jedu tímto způsobem 6 nad 0 


