Matematické Fórum

PL4 · 09. 02. 2013 13:50

Zdravím, mám krychli ABCDEFGH, a = 4cm, a mám určit vzdálenost H, 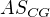$AS_{CG}$ . Je to úloha z Petákové, ve výsledcích je 4cm, ale mě vychází zhruba 4,2. Postupuju takhle:
Střed hrany CG označím třeba S, pak udělám pravoúhlý průmět bodu H na AS, průsečík pojmenuji M. Pak by tedy trojúhelníky MSH a HSA měly být podobné. Z toho vychází poměr: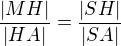
$\frac{|MH|}{|HA|}=\frac{|SH|}{|SA|}$

tj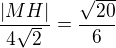

$\frac{|MH|}{4\sqrt{2}}=\frac{\sqrt{20}}{6}$

takže $|MH|=\frac{4\sqrt{10}}{3}$ .

Co je špatně? Moc díky.

Bati · 09. 02. 2013 14:08 — Editoval Bati (09. 02. 2013 14:22)

Ahoj,
ty trojúhelníky nejsou podobné, protože trojúhelník HSA nemá žádný pravý úhel (velikost úhlu AHS je jistě menší než 90 st.).

PL4 · 09. 02. 2013 15:10

No jo :), díky.

PL4 · 09. 02. 2013 16:11

V tom případě radši spočítám délku všech stran trojúhelníku HAS, pak pomocí kosinové věty spočítám úhel u vrcholu A, vyjde 45 stupňů. No a pak už vím, že 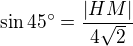$\sin 45^\circ =\frac{|HM|}{4\sqrt{2}}$ , tj ty 4 cm. Ještě jednou díky, já té své 3D představivosti nemůžu věřit.

Matematické Fórum

#1 09. 02. 2013 13:50

Stereometrie vzdálenost bodu od přímky

#2 09. 02. 2013 14:08 — Editoval Bati (09. 02. 2013 14:22)

Re: Stereometrie vzdálenost bodu od přímky

#3 09. 02. 2013 15:10

Re: Stereometrie vzdálenost bodu od přímky

#4 09. 02. 2013 16:11

Re: Stereometrie vzdálenost bodu od přímky

Zápatí