Matematické Fórum

Panassino · 12. 02. 2013 21:35

Zdravím,
mám zadání:
$x^{2}-7x+12<|x-4|$
$x\in \mathbb{R}$

Rozdělil jsem si příklad na 2 fce:
$f:y=x^{2}-7x+12$
$g:y=|x-4|$
f(x) < g(x)
Zjistil jsem vrchol fce f
V=[3,5;-1/4]
Px=(x=3 v x=4) Py=[0;12]
fce g:
Px=[4;0] Py=[0;4]

Mám trochu binec v tom, jak by výsledek vypadal v grafu.
Prosím znázorníte graficky, jak by to mělo vypadat?

teolog · 12. 02. 2013 21:46 — Editoval teolog (12. 02. 2013 21:46)

↑ Panassino:
Zdravím,

martisek · 12. 02. 2013 21:47

↑ Panassino:

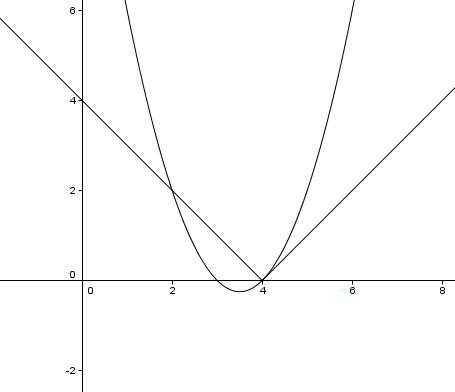
Grafem funkce f je parabola, grafem funkce g dvojice polopřímek se společným počátkem v bodě [4;0]. Řešením nerovnice jsou části osy x, ve kterých je graf g nad grafem f.

martisek · 12. 02. 2013 21:48

↑ Panassino:

S teologem jsme to odpálili téměř současně, jsem rád, že to namaloval (mně se do toho nechtělo :-)

Panassino · 12. 02. 2013 21:54

Děkuji oběma, už to tady taky mám a vyšlo to stejně :)
P(x)=(2;4)

teolog · 12. 02. 2013 21:57

↑ martisek:
Mně se to zase nechtělo popisovat ;)

Matematické Fórum

#1 12. 02. 2013 21:35

Kvadratická fce, fce s absoutní hodnotou

#2 12. 02. 2013 21:46 — Editoval teolog (12. 02. 2013 21:46)

Re: Kvadratická fce, fce s absoutní hodnotou

#3 12. 02. 2013 21:47

Re: Kvadratická fce, fce s absoutní hodnotou

#4 12. 02. 2013 21:48

Re: Kvadratická fce, fce s absoutní hodnotou

#5 12. 02. 2013 21:54

Re: Kvadratická fce, fce s absoutní hodnotou

#6 12. 02. 2013 21:57

Re: Kvadratická fce, fce s absoutní hodnotou

Zápatí