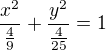Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 02. 2013 13:28
- Matthias

- Místo: -
- Příspěvky: 72
Urči souřadnice elipsy
Zadání:
Urči souřadnice elipsy
Výsledek podle klíče vzadu v učebnici je: ![kopírovat do textarea $[-\frac{8}{15};0][0;\frac{8}{15}]$](/mathtex/65/65e8822ffbb35549e7cb5c32474bea1c.gif)
Jak se to spočítá? Zatím jsem došel pouze ke kroku:

ale asi to bude špatně. Děkuji za rady :)
Berte na mě ohledy, jsem na matematiku prostě úplně blbej :D
Offline
#2 17. 02. 2013 13:33
Re: Urči souřadnice elipsy
↑ Matthias:
Myslím, že si nepresne sformuloval zadanie. O čo ide?
Vrcholy?
Offline

 a
a  , treba upraviť:
, treba upraviť: