Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 01. 2009 00:27
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Mocniny dvojky z hlavy
Dobrý den,
mocniny dvojky byly vždycky mé oblíbené a když jsem teď o Vánocích ležel v posteli nemocen, nějak mě štvalo násobení, když jsem šel od 2^13 k 2^19 z hlavy, protože se mi tam ta čísla všude míchala.
Přemýšlel jsem tak nad zjednodušení, když jen tak chcete vědět, kolik je 2^19 a nemáte po ruce kalkulačku, tužku, ani papír - a navíc bez násobení (částečně). Vycházel jsem z toho, že je jednoduché dostat se k 2^13, protože se ještě nesčítají stovky (2^0 -> 2^10 beru jako zažitou věc).
Celé to vzešlo z toho, že se mi líbilo číslo 2048. To máme 2^0 tisícovek a pak součet 2^5 a 2^4. To samé máme u 1024, 4096 apod.
Vzešel mi z toho tedy jednoduchý vzorec  , případně tedy
, případně tedy 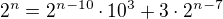 .
.
Příklad:
Což z hlavy není zas tak složité.
Důkaz je jednoduchý, přímým důkazem jsme u 2^n ihned.
---
Chápu, že to nemá žádný matematický význam, ale pokud vás někdy štvalo, kolik je ta vysoká mocnina, nebo jste alespoň přibližně chtěli vědět (stačí tedy  , což je přibližné pro neveliká
, což je přibližné pro neveliká  ) přibližně hodnotu, může se vám to hodit.
) přibližně hodnotu, může se vám to hodit.
Pokud zapomenete vzorec, přes 1024 ho máte odvozený raz dva.
(trochu neprakticky to funguje i pro n < 10)
(na papíře se bude asi více hodit násobení, např.  ;
; 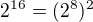 ; ...)
; ...)
Offline
- (téma jako vyřešené označil(a) BrozekP)