Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 02. 2013 22:26
Re: kompaktnost
Kompaktny priestor je casto "pekny" - t.j. funguju tam veci, ktore by inde nemuseli.
1) spojite realne funkcie na kompakte nadobudaju max a min.
(vseobecnejsia verzia je, ze spojity obraz kompaktu je kompakt)
2) kompaktny Hausdorffov priestor je normalny - co je dolezita vlastnost v topologii
3) kompaktny metricky priestor je separabilny
4) sucin kompaktnych priestorov je kompaktny (Tichonovova veta) - dolezite pre funkcionalne priestory (t.j. priestory funkcii) lebo to v podstate hovori, ze priestor funkcii na kompakte (s fix. oborom hodnot) s topologiou bodovej konvergencie je kompaktny
vyuziva to aj Banach-Alaogluova veta ktora ma potom zaujimave dosledky pre reflexivne Banachove priestory
5) Stone-Weierstrassova veta, ktora hovori o aproximacii spojitych funkcii a to, ze spojite realne funkcie na kompakte (to je tu dolezite aj ked sa da zovseobecnit) s topologiou rovnomernej konvergencie su separabilny priestor
Offline
#3 22. 02. 2013 23:39 — Editoval vanok (22. 02. 2013 23:42)
Re: kompaktnost
Ahoj ↑ Honza90:,↑ Brano:
Doplnim trochu predosly prispevok od ↑ Brano:
Pripad metrickeho priestoru je asi najbeznejsi z ktorym sa iste najcastejsie stretnes.
A v takom priestore mame napr tieto vlasnosti
Kazdy kompakt je uzavrety a ohraniceny
V normovanom priestore konecnej dim, uzavrete a ohranicene mnoziny su kompakne
(X, d) kompaktny prave vtedy ak kazda postupnost ma convergentnu podpostupnost
...
( teorema Rietz) Normovany priestor (vseobecnejsie topologicky priestor) je lokalne kompakntny prave vtedu ak je konecnej dim
A mame aj dalsie aplikacie:
Kompaknost a spojitost
Obraz jedneho kompaktu spojitou funkciou je kompaktny
( preto tento obraz je pochopitelne ohraniceny )
Aplikacie
1. kontraktna aprlikacia z jedneho kompaktu do jeho sameho ma FIXNY bod
2. Rolle-ova teorema
3. Darboux-onva teorema
4. Kazda spojita aplikacia z jedneho kompaktu do ineho kompaktu je homeomorfismus
5.Kazda aplikacia z normovaneho priestoru konecnej dim ktora ide k  pre x co sa blizi
pre x co sa blizi
k  je minorovana a existuje bod v ktory je rovny jeho dolnej minoracii
je minorovana a existuje bod v ktory je rovny jeho dolnej minoracii
atd...
Ale na viac:
Mame aj aplikacie Heinovej teoremy:spojita funkcia na kompakte je stejnomerne spojita
potom napr Teorema Ascoli-Arzela ma tiez zaujimave applikacie
Ine aplikacie na kompacitu klasickych topologickych grup
ako napr 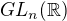
Potom mame aj vlasnosti tykajuce sa konvexity a kompacity
ako napr Teorema Hahn-Banach
a nezabudnime teoremu pevneho bodu (Brouwer)
A nakoniec: Kompakne operatory na Banachovych alebo aj Hibertovych priestoroch... maju zaujimave aplikacie
ako problem Sturn -Liouville
Poznamka:Viac presnosti najdej vdaka napr. google ( a som presveceny, ze toto vsetko budes ovladat na konci tvojho Master)
A napr tiez v knihe od Choquet: topologie najdes uz vela z tychto vysledkov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 23. 02. 2013 00:21 — Editoval Brano (23. 02. 2013 00:38)
Re: kompaktnost
↑ vanok:
Darbouxova veta je skor "spojity obraz suvisleho priestoru je suvisly" nie? Aj ked by sa mozno dalo povedat, ze v standardnej aplikacii do  hra lokalna kompaktnost
hra lokalna kompaktnost  ulohu v dokaze ze suvisle su prave iba intervaly v
ulohu v dokaze ze suvisle su prave iba intervaly v  ... to neviem naisto
... to neviem naisto
---
ale je toho taka kopa co suvisi s kompaktnostou, ze cloveka vsetko ani nenapadne
potom su tu este rozne zovseobecnenia kompaktnosti
- pomerne vyznamna je parakompaktnost - to suvisi s rozkladmi jednotky (kazdy metricky priestor je parakompaktny, tak toto zo zaciatku asi nebude az tak zaujimave)
- uz spominana lokalna kompaktnost
- vo fukcionalke sa objavuju aj varianty ako sekvencialna kompaktnost a spocitatelna kompaktnost ... napr. vo variacnom pocte (optimalizacne problemy)
Offline
#5 23. 02. 2013 00:38 — Editoval vanok (23. 02. 2013 00:56)
Re: kompaktnost
↑ Brano:,
Co sa tyka Darboux, som myslel tuto vetu ( vyuziva kompaktnost a spojitost)
Uvazujme f derivatelnu, potom obraz f '(I) intervalu I, je tiez interval.
Mas pravdu, ze som nebol encyklopedicky a pochopitelne tento zoznam zo tvojou (nasou) spolupracou mozme este obohatit. ... co sa tyka dokazov iste pre kolegu postacia odkazy na literaturu, na co mu mozem, ak chce (alebo potrebuje) dat viacere francuzke zdroje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 23. 02. 2013 01:28
Re: kompaktnost
vanok napsal(a):
Mas pravdu, ze som nebol encyklopedicky a pochopitelne tento zoznam zo tvojou (nasou) spolupracou mozme este obohatit. ...
ach to v ziadnom pripade nebolo myslene ako vycitka - to bolo myslene skor pre honzu, ze toho je proste vela a ze je to naozaj vlastnost hodna pozornosti pri studiu :-)
Offline
#8 23. 02. 2013 01:50
Re: kompaktnost
↑ Brano:
Vsak to neberiem ako vycitku.
Ale tak ci tak spolupraca je uzitocna.
Toto sa mi zda byt zaujimavy pristupny clanok na tuto temu
http://www.math.ntnu.no/conservation/2009/037.pdf
Co si ty o nom myslis?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 23. 02. 2013 11:03
Re: kompaktnost
Vyuzitie tej lemy 1 v uvadzanych klasickych vetach neviem nejak extra ocenit, lebo ziaden z nich okrem A-A nepoznam. Ale samotna lema 1 nie je nic nove.
podmienka: 
znamena, ze 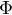 je injektivne a teda ma inverz
je injektivne a teda ma inverz  definovany na
definovany na 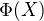 , ktory je rovnomerne spojity.
, ktory je rovnomerne spojity.
A je dobre zname, ze rovnomerna spojitost zachovava totalnu ohranicenost, (resp. ekvivalentne ze zachovava Cauchyovskost siete).
Offline

 et g la fonction définie sur T par
et g la fonction définie sur T par 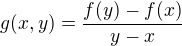 .
.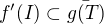 (par définition de la dérivée) et le théorème des accroissements finis dit exactement que
(par définition de la dérivée) et le théorème des accroissements finis dit exactement que  .
.