Matematické Fórum

JohnPeca18

Ahoj, vedeli by ste mi pomoct?
uloha

Zatím mám jenom a), tam stačí zobrať i v 2 kovej sustava a doplnit zľava nulami na n-ciferne cislo. Vezmem postupnost
n bitov a pokiaľ bude ostre menšia ako i, tak odpoviem ANO, inak NIE.
b) a c) zatim nevim . .

Stýv · 02. 03. 2013 21:11

jestli jsem to správně pochopil, tak např. pro x=1/3 bych přečetl 2 bity. v případě:
11 vrátím ano,
10 a 01 vrátím ne,
00 přečtu další dva bity a opakuju...

JohnPeca18 · 02. 03. 2013 21:18

↑ Stýv:
hm, to nevim jestli vychazi, to by byla pravdepodobnost ano
$\frac{1}{4}+\frac{1}{4}(\frac1 4+\frac{1}{4}(\dots))$
Myslíš, že to dáva dokopy 1/3?

Stýv · 02. 03. 2013 21:43

jasně. buď to sečti jako geometrickou řadu, nebo to vem tak, že psti ano:ne jsou 1:2, tedy 1/3 a 2/3

JohnPeca18 · 02. 03. 2013 22:50

Hm, dobra dekuji, vychazi to. Jeste je potreba vypočítať priemerný prípad. Najhorší prípad bude, že potrebujem nekonecno bitu, coz není kdoví co.

Stýv · 03. 03. 2013 01:26

doporučoval bych využít geometrický rozdělení

JohnPeca18

Neviem čo si ale predstaviť pod priemerom, skor ted počítam strednú hodnotu.
Nech teda x je racionálne číslo 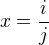$x=\frac i j$ . Potom nájdem n, také že $2^n\geq j$ .
Vygenerujem n náhodných bitov. Vzniknuté číslo v 2-kovej sústave označím $y,0\leq y\leq 2^n-1$
Ak $0\leq y < i$ odpoviem ANO ak $i\leq y < j$ odpoviem NIE. Inak vezmem dalsich n bitov a opakujem.

$P(ANO)=\frac{j}{2^n}.\frac{i}{j}+(1-\frac{j}{2^n})(\dots)=\sum_{k=0}^{\infty}\frac{j}{2^n}.\frac{i}{j}.(1-\frac{j}{2^n})^k=\frac{j}{2^n}.\frac{i}{j}\frac{1}{1-(1-\frac{j}{2^n})}= \frac{i}{j}$

$n\leq E(bitov)= \sum_{k=1}^{'\infty}kn(1-\frac{j}{2^n})^{k-1}(\frac{j}{2^n})= n\sum_{k=1}^{'\infty}k(1-\frac{j}{2^n})^{k-1}(\frac{j}{2^n})=$
$\frac{n}{1-\frac{j}{2^n}}\sum_{k=1}^{'\infty}k(1-\frac{j}{2^n})^k(\frac{j}{2^n})= \frac{n}{1-\frac{j}{2^n}}\frac{1-\frac{j}{2^n}}{\frac{j}{2^n}} \leq \frac{n}{\frac 1 2}=2n$

Mohlo by to byt takto? hlavne mi ide o to pouzitie geometrickeho rozdelenia, ci to je dobre.
A tiez zostava vymysliet nieco na to c). Reprezentacia iracionalneho cisla x, pry muze byt pomoci
funkce ktora pre kazde racionalne cislo y vraci, jestli y<x alebo y>x.