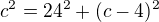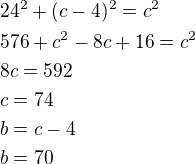Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2009 17:59
- cartersam1
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Úlohy s rovnicemi
Ahoj, potřebovala bych moc pomoci s řešením těchto slovních úloh s rovnicemi. Bohužel si s tím nevím rady. Díky moc všem, kteří pomohou. (Pokud byste byli tak hodní, a sestavili rovnici :-))
1. Určete dvě čísla, z nichž jedno je o 10 větší než druhé, víte-li, že rozdíl druhých mocnin obou čísel je 400.
2. Číslo 57 rozdělte na dvě čísla taková, aby rozdíl druhých mocnin byl zase 57.
3. Číslo 100 rozdělte na dvě čísla taková, ay součet druhých mocnin byl o 2800 větší než dvojnásobek druhé mocniny menšího z obou.
4. Obvod trojúhelníka je 104 cm. Jedna jeho strana je o 6 cm delší než druhá a o 8 cm kratší než třetí strana. Určete délky stran.
5. V obdelníku je jedna strana o 20 cm delší než druhá. Zkrátí-li se delší o 5 cm a zároveň prodlouží kratší o 10 cm, vzroste obsah obdélníka o 300 cm2. Jaké jsou rozměry původního obdelníka?
6. Kolik litrů vody 48°C teplé je nutno přidat do 1,2 hl vody 8°C teplé, aby směs měla teplotu 24°C?
7. Jedna odvěsna pravoúhlého trojúhelníka je 24, druhá odvěsna je o 4 menší než přepona. Určete velikosti neznámých stran.
8. Z místa A vyjde chodec rychlostí 6 km/h, z místa B vzdáleného 27 km od A v opačném směru vyjede současně s ním cyklista rychlostí 24 km/h. Kdy a kde ho dohoní?
9. Ze dvou míst vzájemně 285 km vzdálených vyjela dvě nákladní auta proti sobě; první ujede za hodinu 30,5 km; druhé 40,75 km. Kdy se potkají?
10. Dva chodci A, B jsou od sebe vzdáleni 57,2 km a vyjdou si současně vstříc. Když se sejdou, shledají, že A ušel o 4,4 km více, což je způsobeno tím, že ujde za hodinu o 0,8 km více. Po které době se setkali? Jak jdou rychle?
11. Deset studentů vysoké školy slíbilo, že roztřídí a zalepí do obálek materiály k přípravě na přijímací zkoušky pro 1 500 uchazečů o studium. Každému studentu by celá práce trvala 50 hodin. Čtyři začali pracovat v 8 hodin ráno, čtyři v 9 hodin a dva až v 11 hodin. Kdy byli s prací hotovi, jestliže si v poledne udělali hodinovou přestávku na oběd?
Díky moc za pomoc!
Offline
#2 05. 01. 2009 18:08 — Editoval O.o (05. 01. 2009 18:11)
Re: Úlohy s rovnicemi
↑ cartersam1:
Ahoj .),
máš nějaké pokusy o sestavení (ikdyby nesprávné, tak lepší než nic)?
Add 1) 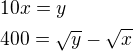
Je možné něco takového (pokud ano, tak obdobně u dalšího příkladu, atp.)?
Add 8-11) Úlohy o pohybu a společné práci (tedy nečetl jsem to celé, jen začátek zadání, tak pokud je tam nějaká zrádnsot, tak se omlouvám .)), pod těmito názvy tu toho najdeš spousty (obzvláště jsou tyto příklady oblíbené u řešitelek Ivana, jelena - tímto obě zdravím .)).
Offline
#3 05. 01. 2009 18:19
Re: Úlohy s rovnicemi
↑ cartersam1:
ad1)
První číslo - x
Druhé číslo - x + 10
Pak lze sestavit rovnici: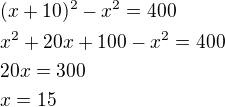 první číslo
první číslo
Druhé číslo je dle zadání x + 10 = 15 + 10 =25
Hledaná čísla jsou 15 a 25
Offline
#5 05. 01. 2009 18:25
Re: Úlohy s rovnicemi
↑ cartersam1:
ad2)
Hledaná čísla označíme x,y
Pak lze psát: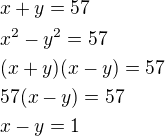
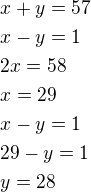
Hledaná čísla jsou 29 a 28
Offline
#6 05. 01. 2009 18:31 — Editoval Chrpa (05. 01. 2009 22:26)
#7 05. 01. 2009 18:38
Re: Úlohy s rovnicemi
↑ cartersam1:
ad4)
Jedna strana bude a.
Druhá bude a - 6
Třetí bude a + 8
Pak píšeme:
Druhá strana a - 6 = 34 -6 = 28
Třetí strana a + 8 = 34 + 8 = 42
Strany trojúhelníku jsou: 28, 34, 42
Offline
#8 05. 01. 2009 18:58
#11 05. 01. 2009 19:03
#14 05. 01. 2009 19:35
Re: Úlohy s rovnicemi
↑ cartersam1:
ad 10)
Ze zadání musí platit:
1) 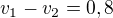 rychlejší jde rychlostí v_1 km/h pomalejší rychlostí v_2 km/h
rychlejší jde rychlostí v_1 km/h pomalejší rychlostí v_2 km/h
2) 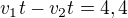 t je čas, za ktarý se potkají
t je čas, za ktarý se potkají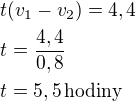
Setkají se za 5 a půl hodiny.
Musíme ještě určit rychlosti:
Rychlosti chodců jsou 5,6 resp. 4,8 km/h
Offline
#15 05. 01. 2009 19:44
- cartersam1
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Úlohy s rovnicemi
Jé, moc vám děkuju! To by mě v životě nenapadlo na to přijít! Moc, moc děkuju Vám všem!
Offline
#16 05. 01. 2009 20:02 — Editoval Chrpa (05. 01. 2009 20:04)
Re: Úlohy s rovnicemi
↑ cartersam1:
ad 11)
Počítal bych to takto (zapojíme selský rozum - já můžu, protože dělám v zemědělství)
Možná na to jde napasovat nějaká rovnice, ale jsem už líný ji vymýšlet.
Tak tedy:
od 8 do 9 hodin pracovali 4 studenti a za 1 hodinu bylo hotovo 4/50 úkolu.
od 9 do 11 hodin pracovalo 8 studentů a za tyto dvě hodiny udělali 2*8/50 = 16/50 úkolu.
od 11 do 12 hodin, než šli na oběd pracovalo 10 studentů a udělali 10/50 = 1/5 úkolu.
Do 12 hodim tak bylo hotovo: 4/50+16/50+10/50 = 30/50 = 3/5 úkolu.
Od 12 do 13 hodin nikdo nic neudělal.
od 13 hodin až do konce práce muselo všech 10 studentů dodělat 1-3/5 = 2/5 úkolu
Protože 1/5 úkolu udělalo 10 studentů za 1 hodinu, pak 2/5 úkolu dělalo 10 studentů 2 hodiny
S prací tedy byli studenti hotovi v 13 + 2 = 15 hodin
Odpověď
Ükol byl splněn v 15.00 hodin.
Offline
#17 05. 01. 2009 20:04
- cartersam1
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Úlohy s rovnicemi
Můžu vás ještě poprosit o vypočítání 5 ? Díky
Offline
#18 05. 01. 2009 20:09
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Úlohy s rovnicemi
↑ cartersam1:
Zkus to taky sám, alespoň nějaký pokus.
Offline
#19 05. 01. 2009 20:12 — Editoval Chrpa (05. 01. 2009 20:18)
Re: Úlohy s rovnicemi
↑ cartersam1:
ad5)
Kratší strana obdélníku bude - a
Delší strana pak - a+20
Sestavíme rovnici: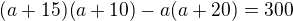 to je vyjádření rozdílu v obsazích obdélníků
to je vyjádření rozdílu v obsazích obdélníků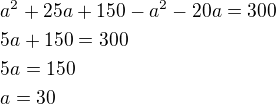
Kratší strana má 30 cm.
Delší strana je a + 20 = 30 + 20 = 50 cm
Rozměry obdélníka jsou 50 cm a 30 cm.
PS výraz (a+10) jsme dostali tak, že jsme kratší stranu prodloužili o 10 cm
výraz (a+15) jsme dostali tak, že jsme delší stranu zkrátili o 5 cm tj a + 20 - 5 = a + 15
Offline
#20 05. 01. 2009 20:48
- cartersam1
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Úlohy s rovnicemi
Ahoj! Všem vám ještě jednou děkuju za výpočty.
Teď jsem zkoušela počítat toto zadání: V kolik hodin vychází Slunce počátkem května, tvoří-li noc 17/22 ze 24 hodin a Slunce zapadá v 19 h 20 min?
Začala jsem řešit: 17/22*24+19,20=x
to mi ale nevychází!
Offline
#21 05. 01. 2009 20:49 — Editoval Chrpa (05. 01. 2009 20:49)
Re: Úlohy s rovnicemi
↑ cartersam1:
ad8)
čas, za který se potkají bude t.
Sestavíme rovnici: jedou proti sobě a dohromady za čas t ujedou vzdálenost AB = 27 km
jedou proti sobě a dohromady za čas t ujedou vzdálenost AB = 27 km
Setkají se za 54 minut.
Chodec jdoucí z A rychlostí 6 km/h ujde za čas t: 6*9/10 = 5,4 km
Setkají se tedy za 54 minut ve vzdálenosti 5,4 km od místa A.
Offline
#22 05. 01. 2009 21:58 — Editoval Chrpa (05. 01. 2009 21:58)
Re: Úlohy s rovnicemi
↑ cartersam1:
Určitě je to zadání dobře?
Nemá být v zadání, že den tvoří 17/22 z 24 hodin?.
Protože pokud by zadání bylo dobře, pak by Slunce vycházelo
ve 13 hodin 52 minut a 43 vteřin, což je z praktického hlediska nesmysl.
Offline
#23 21. 02. 2021 10:37
- Vít Hrdlička

- Zelenáč
- Příspěvky: 1
- Škola: SSPTAJi
- Pozice: Student
- Reputace: 0
Re: Úlohy s rovnicemi
Dobrý den, potřeboval bych vyřešit úlohu č. 3 , ale pouze s jednou neznámou, podle učitelky to nějak jde. Níže ještě jednou zasílám zadání. Předem děkuji Vít
3,Číslo 100 rozdělte na dvě čísla taková, ay součet druhých mocnin byl o 2800 větší než dvojnásobek druhé mocniny menšího z obou.
Offline
#24 21. 02. 2021 11:11
Re: Úlohy s rovnicemi
↑ Vít Hrdlička:
Prostě si zadání přepiš do rovnice. Když  , tak
, tak
V čem je problém?
A příště si založ vlastní téma.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
 a číslo
a číslo 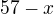 . Napiš si jejich druhé mocniny do rozdílu a dopočítej.
. Napiš si jejich druhé mocniny do rozdílu a dopočítej.