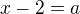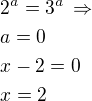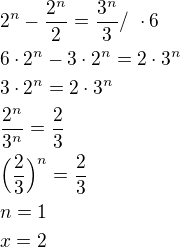Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Jednoduchá exponenciální rovnice... (TOTO TÉMA JE VYŘEŠENÉ)
#6 06. 01. 2009 16:22 — Editoval ttopi (06. 01. 2009 16:23)
Re: Jednoduchá exponenciální rovnice...
Už tam skoro jsi... teď jen vynásobit 6 a pak už to pujde ne? Nakonec dáš na jednu stranu výrazy s y, na druhou stranu jen čísla...
Tady je pak výsledek
oo^0 = 1
Offline
#8 06. 01. 2009 16:31
Re: Jednoduchá exponenciální rovnice...
Tak to si mi moc nepomohl, výsledek tu mám taky na papíře :D Já bych potřeboval spíš trknout, jak se řeší příklad s ruznýma základama mocnin. Pokud jsou základy stejný, nečiní mi exponenciální rovnice žádnou potíž, ale jsou různý, tak mi to pořád nějak nejde do hlavy :(
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Jednoduchá exponenciální rovnice... (TOTO TÉMA JE VYŘEŠENÉ)


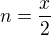 .
.

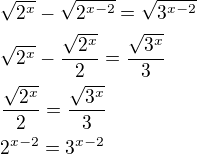 substituce
substituce