Matematické Fórum

jelena · 11. 03. 2013 21:54

↑↑ Martass:

Děkuji za zprávu, požadavek na nalezení souřadnic na oblouku byste měl mít komplet ↑↑ příspěvek 24:. Tak se potom ozvete, zda je všechno, jak má. Časově to je všelijak a asi k samotnému dokončení programu těžko přispěji, ale pokud byste narazil na nějakou nesrovnalost v předchozím výpočtu, tak bych se ještě zapojila.

Ať se podaří.

Martass · 11. 03. 2013 22:22

↑ jelena:
Dobrý večer!
Já děkuji Vám.U mě je to teď s časem také všelijak,před chvíli jsem dorazil z rachoty,takže než to celé zkompletuji to bude chvíli trvat,
ráno jsem první část s m,n zařadil úspěšně do programu,teď z toho musím ještě vydolovat
úhly těch koncových bodů.Tak mám co dělat.Samozřejmě přispěji na provoz SMS,už jste mi tady hodně pomohly
a neměla jste to se mnou vůbec lehké.....!
Ještě jednou děkuji,mějte se hezky

Martass · 15. 03. 2013 10:54

Dobrý den!
Tak jsem zpět,každý den se snažím příjít na to co dělám špatně,co jsem nepochopil atd.,jsem zmaten....
Pořád mi není jasný výpočet z příspěvku č.24 x1,2=
Protože pokud dosadím a vypočítám hodnoty do této rovnice podle příspěvku. č.21

z toho vyjde A=50 B=-1 m=50 n=50 (malý,červený oblouk)

$x_{1, 2}=\pm \sqrt{\frac{R^2}{1+B^2}}+m$
$x_{1,2}=\pm \sqrt{\frac{100^{2}}{1+(-1)^{2}}}+50$

výpočet ve wolframu Odkaz ,tak mi vycházejí pro mě nepochopitelné výsledky (x=120.7 ???) co ta hodnota tedy znamená?Co zase dělám špatně?Co jsem nepochopil?
Děkuji

jelena · 15. 03. 2013 13:11

↑ Martass:

Zdravím Vás,
podle mne to je v pořádku - je to x-souřadnice bodu uprostřed malého červeného oblouku (na Vášem obrázku bude nad nápisem R100). Pokud dáte minus před odmocninu, tak dostanete x-souřadnici bodu středu na velkém modrém oblouku. Tedy jsou to body, co jsou uprostřed na obloucích kružnice se středem 50, 50.

y- souřadnici ještě třeba dopočíst (pokud třeba).

Martass · 15. 03. 2013 21:00

↑ jelena:
Takže pokud to dobře chápu tak tímto výpočtem určuji, zda budu dělat,modrý nebo červený oblouk,je tak?

jelena · 15. 03. 2013 23:17

↑ Martass:

nám to nějak vazně, ale už se diskutuje sekce pro praxi, tak snad se dostanete do lepších rukou :-)

m=50 n=50 (malý,červený oblouk)

to je střed kružnice, která má část "malý červený oblouk" (a také velká modrý oblouk")

z toho vypočtu $x_{1, 2}=\pm \sqrt{\frac{R^2}{1+B^2}}+m$ dostanete 2 různé hodnoty na ose x:

$x_{1}=+\sqrt{\frac{100^{2}}{1+(-1)^{2}}}+50$
$x_{2}=-\sqrt{\frac{100^{2}}{1+(-1)^{2}}}+50$

Na obrázku jsem zeleně vyznačila, do kterých bodů na oblouku se takto dostanete (a konkrétně, kde je x1 na ose x - zeleně jsou osy souřadnic).

A ano - když se rozhodnete zvolit + před odmocninou, tak jste na červeném oblouku, když zvolíte - před odmocninou, tak jste na velkém modrém oblouku.

Vám se teď nezdá výpočet, nebo že není jasné jak postupovat dál a jak zvolit konkrétní oblouk? Děkuji, věřím, že se pohneme.

Martass · 15. 03. 2013 23:51

↑ jelena:
Já vím ,nemáte to se mnou lehké!!
Nevím jak přesně definovat co myslím,ale pokusím se....
Toto vše je mi jasné,ale jsem jaksi zaseknutý na tomto.
Myslel jsem ,že pokud pro výpočet bodu m použiji 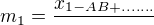$m_{1}=\frac{x_{1-AB + .......}}{}$ ,tak počítám vždy velkou kružnici a pokud použiji $m_{2}=\frac{x_{1-AB - .......}}{}$ ,tak počítám vždy malou kružnici,ale ono to tak asi není,co?Alespoň mám případ kde to je obráceně a tak vlastně předem nevím kdy použít minus a kdy plus.....

jelena · 16. 03. 2013 00:14

↑ Martass:

to ne, že není lehké, to se pohne :-)

Řekla bych, že:

a) volbou 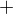$+$ před odmocninou v rovnici pro střed $m$ se dostáváte napravo od souřadnice $x_1$ (1. zadaný okraj oblouku).
$m_{1,2}=\frac{x_1-AB\pm \sqrt{(AB-x_1)^2-(1+B^2)(x_1^2+A^2-R^2)}}{1+B^2}$ .

b) volbou 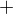$+$ v souřadnici pro středový bod na oblouku (označím ho raději velké X) $X_{1, 2}=\pm \sqrt{\frac{R^2}{1+B^2}}+m$
se dostáváte napravo od středu kružnice.

Obdobně s volbou minusů, nebo i s volbou kombinací plus pro střed, ale minus pro oblouk a naopak.

Zkuste to tak překontrolovat - tedy Vy budete mít možnosti od zadané úsečky zvolit směr, kde bude budoucí střed kružnice. A od tohoto středu ještě zvolíte směr - kde bude budoucí oblouk (a bod na oblouku). Vychází to?

Mé psání třeba číst nahlas - píši to tak, jak povídám, to se omlouvám.

Martass · 16. 03. 2013 00:53

↑ jelena:
Netřeba se omlouvat,zatím vždy je problém jenom u mě.....
Tak teď je mi to už trochu jasnější,děkuji za vysvětlení,pokusím se nějak dát tyto podmínky
do mého programu.Uvidím jak mi to půjde,jsem si přitáhl z práce bacila,tak víte jak to my kluci
težce snášíme, kašílek a rýmička a jsme na umření.....
Zatím opět děkuji,uvidím co vymyslím,ale řekl bych,že se ještě ozvu...!!!
Příjemný víkend

Martass · 13. 09. 2023 18:24

Ahoj,
po delší odmlce bych vás tady chtěl požádat o další pomoc.
Jedná se podobný problém který jsem řešil v tomto vláknu a který ke spokojensti využívám.
Jenže teď řeším opět souřadnice středu na oblouku,ale s tím rozdílem,že se pohybuji ve všech kvadrantech jak na
startovní pozici(X1,Y1) ,tak i koncový bod (X2,Y2) může končit v jakémkoliv kvadrantu.
Oblouk může být pouze v jednom kvadrantu,ale může být i přes tři kvadranty.
Původně jsem myslel,že pomocí určení bodů X1,Y1,X2,Y2 jsem schopen jednoduše určit v kterém kvadrantu se pohybuji,ale
nějak to takto asi nejspíš nejde!
Předem znám počáteční i koncové body oblouku, znám směr oblouku a oblouk bude vždy velký,tím se zužují možnosti
na jednu možnost z těch původních čtyř (pokud se nepletu).
Děkuji za případnou pomoc
Martin

Bati · 13. 09. 2023 18:53

↑ Martass:
Ahoj,
pri letmem pohledu na to 10 let stare vlakno me napada otazka: Proc nepouzijes polarni souradnice?

Martass · 13. 09. 2023 21:16

Děkuji za odpověď,
ale ani polární souřadnice mi moc neříkájí (i když jsem se to snažil vygoglit...)

Matematické Fórum

#26 11. 03. 2013 21:54

Re: střed oblouku

#27 11. 03. 2013 22:22

Re: střed oblouku

#28 15. 03. 2013 10:54

Re: střed oblouku

#29 15. 03. 2013 13:11

Re: střed oblouku

#30 15. 03. 2013 21:00

Re: střed oblouku

#31 15. 03. 2013 23:17

Re: střed oblouku

#32 15. 03. 2013 23:51

Re: střed oblouku

#33 16. 03. 2013 00:14

Re: střed oblouku

#34 16. 03. 2013 00:53

Re: střed oblouku

#35 13. 09. 2023 18:24

Re: střed oblouku

#36 13. 09. 2023 18:53

Re: střed oblouku

#37 13. 09. 2023 21:16

Re: střed oblouku

Zápatí