Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » inverzné riešenia diferenciálnych rovníc (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 03. 2013 10:44 — Editoval jarrro (10. 03. 2013 10:45)
inverzné riešenia diferenciálnych rovníc
ahoj
musia vždy existovať nejaké riešenia diferenciálnych rovníc
a
(efy sú v oboch prípadoch tie isté)
a interval tak, že na tom intervale sú tie riešenia navzájom inverzné funkcie?
podľa mňa ak tie rovnice majú zmysel (nevyskytuje sa delenie nulou a podobné matematické nezmysly) a riešenie na nejakom spoločnom intervale
tak áno,lebo
teda máme diferenciálnu rovnicu pre funkciu x premennej y preznačením y a x dostaneme druhú rovnicu
je niekde nejaký zádrheľ
?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#3 10. 03. 2013 19:35
Re: inverzné riešenia diferenciálnych rovníc
↑ martisek:všimni si tie prehodené argumenty
MATH IS THE BEST!!!
Offline
#4 10. 03. 2013 23:08
Re: inverzné riešenia diferenciálnych rovníc
↑ jarrro:
Tak toho jsem si opravdu nevšiml, ale ani tak se mi to nezdá. Vezměme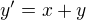
Řešením je např. 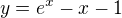 , inverze je
, inverze je 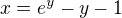 , dosazeno do
, dosazeno do
dává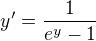
což mi jako identita rozhodně nepřipadá.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#5 11. 03. 2013 07:34 — Editoval jarrro (11. 03. 2013 07:41)
Re: inverzné riešenia diferenciálnych rovníc
↑ martisek:inverzné riešenie dáva 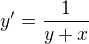
funkcia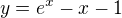
nemá elementárnu inverznú je vyjadriteľná len pomocou Lambertovej funkcie
http://www.wolframalpha.com/input/?i=y% … 28y%2Bx%29
MATH IS THE BEST!!!
Offline
#7 11. 03. 2013 12:17
Re: inverzné riešenia diferenciálnych rovníc
↑ jarrro: ↑ pf:
Vidím, že mi to včera s blížící se půlnocí už nějak nemyslelo. Teď nad jsem nad tím znovu zapřemýšlel a musím uznat, že to vypadá logicky. Navíc by "přechod k inverzní funkci" mohl být zajímavou metodou řešení některých typů rovnic 1. řádu.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#8 05. 04. 2013 10:24 Příspěvek uživatele OiBobik byl skryt uživatelem OiBobik. Důvod: chybka
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » inverzné riešenia diferenciálnych rovníc (TOTO TÉMA JE VYŘEŠENÉ)

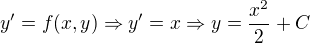
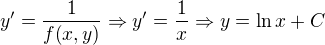
 daná implicitně rovnicí
daná implicitně rovnicí 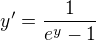 .
.