Matematické Fórum

a co bys rád?

O je obvod?

TAkhle to je zadáno
Sestroj trojuhelnik ABC kde obvod=12cm,Vc=3cm,|<ACB|=60°
nic vic tam neni!!!
zkoušel jsme to přes euklidovu větu a jde to je to delší ale při konstrukci nejde vypočítávat a pomáhat si vysledkama z počítání...!!!

tu mnozinu bodu jsme zkousel taky ale nevime zakladnu zejo...takze jsme to zkusil s tema 12cm a to vyjde ze je tupouhlej ....
taky nevim co stim

Trojuhlenik neni tupouhly a v zadani nemuze byt, o jaky trojuhlenik jde, protoze to by bylo uz moc podminek najednou. Jen pro informaci - kdyz preznacim strany tak, abych znal vysku na stranu 'a', pak to hledane vypada takto:



Vypocet by mohl jit treba timto smerem:

Oznacne pomerne standardne s = (a+b+c)/2 = 6 podle zadani. Pak plati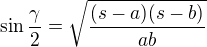

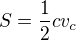. Tim jsme dostali do hry obvod a uhel gamma. Ted jeste nejak tu vysku - na to se skoro vzdycky hodi obsah: pro obsah trojuhelnika je . Samozrejme je tez , kde .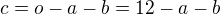

Ze vzorce pro polovicni gammu dostaneme 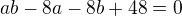a z porovnani obsahu mame 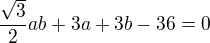. Kdyz prvni rovnici vynasobim 3/8 a sectu se druhou, vypadnou linearni cleny a dostanu, ze , kde je konkretni cislo. Dosazeno do nektere z rovnic to dava kvadratickou rovnici - tedy budou dva (vzajemne symetricke) trojuhleniky, coz jsme stejne cekali.

Jak ale udelat sikovnou kontrukci, ktera jen slepe nekopiruje vyse uvedeny vypocet, zatim nevim...

↑ pusik1989:

Zdravím :-)

Pokud je zadaný obvod, tak to obvykle postaveno na použití osové symetrie:

http://forum.matweb.cz/upload/475-obvod.JPG

Je potřeba překontrolovat úhly, ale snad je to v poradku. Je tomu rozumět?

↑ pusik1989:

"Náčrtek hezký" - to je úžasné hodnocení, na to budu moc pyšná :-)

Vycházime z toho, že původní trojúhelník "rozbalime" - stříhneme ho ve vrcholu C a celý obvod nakreslíme jako přímku C´C´´. Když jsme trouhleník rozbalili, tak strana C´A je stejna jako CA, strana C´´B je stejná jak CB, uhly k alfa, k beta pomyslně dopočitávam do 180 stupnů.

Nic z toho pochopitelně nemáme, pouze to použíjeme pro rozbor a dopočet úhlu, ktery jsem označila v pravém horním rohu, ten vjadřujeme přes gama.

Trojuhelníky C´AC a BC´´C jsou rovnoramenné, trochu si pohrej s vyjadřováním úhlů tak, aby nezůstalo alfa, beta, ale pouze gama.

Nakonec kreslíme trojuhelník C´C´´ C - který je určitý - máme základnu C´C´´, úhel při vrcholu a výšku, kterou jsem nenakreslila, abych nezaplacavala svůj hezký náčrtek. Spojime C´C a vytvoříme osu úsečky, stejně tak C´´ C a opět osa úsečky. Kde se osy protnou se základnou skutečně vznikně bod A, B

Já se moc omlouvám, mám moc málo časů. třeba se toho výkladu ujme někdo z kolegů, děkuji :-).

OK?

↑ pusik1989:

Nebude ALE, ani alfa, ani beta.

Nakreslis C´C´´ dlouhe 12 cm (obvod), nakresliš rovnoběžku ve vzdálenosti vyšky (ekvidistantu).

Nakresliš množinu bodů, ze které vidiš úsečku C´C´´ pod úhlem, jak jsem dopočítala v pravém horním rohu (90 +c/2) - ten dopočet ještě zkontroluj, jestli jsem nepřehodila nejaké znaménko.

Budeš mít trojuhelník C´C´´ C uděláš osy useček C´C a C´´C a kde se osa protné s úsečkou C´C (to je ta základna), tam budou body A, B.

Já rozumím, že to vysvětluji moc hopem, ale opravdu, pokud je zadan obvod, snaz se se zaměřit na osovou symetrii. OK?

↑ jelena:
Ted jsme to zkousel a vubec to nevychazi dal jsme mnouzinu bodu pod kterou je videt ta C´a C´´ a ta kruznice je mimo tu usecku a tu rovnobezku Vc to protina az nekde vzadu a kdyz je teda
(90 +c/2) tohel 120° tak to dam jako 30° a pak kolmici vytvorim tu mnozinu ale nechapu jak ti tohle mohlo vyjit . ja myslim ze ty jdes na to dobre, ale asi si dostatecen neuvedomuj ten princip tech uhlu oni muzou byt jaky koliv a jedinej uhel je Gama a stim se neda dopocitat alfa ani beta.

Děkuju móóóóóóóócccccccccccccccccccccccccc :-*