Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Zvlášnosti matematiky aneb 1 + 1 = 1 (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 01. 2009 15:04
Zvlášnosti matematiky aneb 1 + 1 = 1
Napr. zo života: Čo v živote existuje 1 celok + 1 celok sa rovná = 1 celok;Resp. 1 celok + 1 celok = 3 ?...Jedna žena,jeden muž a jedno decko =D... ešte veľa takýchto "problémov" existuje v matike...
Matematiku nemám rád - je to veda o nekonečnom,narozdiel od fyziky - fyzika je len taká veľká ako priestor...moje myslenie...
Najkratšie odpovede – áno a nie – vyžadujú najdlhšie rozmýšľanie.Pythagoras
Offline
#2 08. 01. 2009 16:12
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Laik:
Toto nejsou problémy v matematice nebo s jejím aparátem, ale problémy v jeho pochopení. Mám pocit, že mícháš jablka hrušky dohromady. Pokud píšeš "rovnici" 1 celok + 1 celok sa rovná = 1 celok, pak to není zcela v pořádku, protože na každé straně se jedná o takový celek, který má nebo může mít jiný relativní vztah k ostatním cekům či nadcelkům. Jednodušeji řečeno, není celek jako celek. O rovnítku nemá smysl hovořit, protože kvantita na levé a pravé straně si z daného aspektu nevyhovují. Chci-li něco srovnávat, nebo dokonce prohlásit o kvantitách A a B, že se rovnají, musím porovnávat skutečnosti, které má smysl porovnávat a především porovnávat nebo hodnotit ze stejného aspektu.
Nejsou to tedy problémy v matematice, ale spíše nedůslednost studentů a jejich problémy tyto nedůslednosti pochopit a třeba i odstranit (je-li dost vůle).
Offline
#3 08. 01. 2009 16:21
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1853
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
Není spíš problém v jednotkách? Má tenhle zápis smysl? 50 + 50 = 1. Takhle asi ne, ale 50 cm + 50 cm = 1 m. Takhle už jo. Stejný problém je při celcích. Jeden celek čeho?
2+2=4
Offline
#5 08. 01. 2009 17:39
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
Jedno Vajce (celok) = 1 bílko + 1 žloutek =D aneb kuchynská věda v matice =D;
Matematiku nemám rád - je to veda o nekonečnom,narozdiel od fyziky - fyzika je len taká veľká ako priestor...moje myslenie...
Najkratšie odpovede – áno a nie – vyžadujú najdlhšie rozmýšľanie.Pythagoras
Offline
#7 08. 01. 2009 18:21
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
A čo toto: Dvaja členovia rodiny - Muž a žena;(1+1)...po pár rokoch: Traja členovia rodiny: Muž,žena a dieťa.(1+1+1)...kde v tejto zapeklitej situácií nájdete východisko?... 2 != 3
Matematiku nemám rád - je to veda o nekonečnom,narozdiel od fyziky - fyzika je len taká veľká ako priestor...moje myslenie...
Najkratšie odpovede – áno a nie – vyžadujú najdlhšie rozmýšľanie.Pythagoras
Offline
#9 08. 01. 2009 19:24
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
Laik si tady z nas dela nepokryte srandu. Na druhou stranu ale, kdo rika, ze se neda vybudovat konzistentni teorie, ktera nesplnuje prepoklad, ze celkovy objem dvou teles neni stejny jako soucet jejch objemu.
Potom klidne muze by napriklad 1 + 1 = 1,5
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#10 08. 01. 2009 19:34
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Lishaak:presne...snažil som sa im to trošičku vysvetliť okľukou a chcel som aby im to došlo...ide o látkové množstvo,látkové vlastnosti,...napr. papier,keby ste tonu papiera namočili do vody tak,aby už viacej vody nenasiaklo a keďže ste pridali rovnaký objem papiera a vody -> váhu by to malo (dám blud) 1,8t...a nie 2t...teda 
Matematiku nemám rád - je to veda o nekonečnom,narozdiel od fyziky - fyzika je len taká veľká ako priestor...moje myslenie...
Najkratšie odpovede – áno a nie – vyžadujú najdlhšie rozmýšľanie.Pythagoras
Offline
#11 08. 01. 2009 22:12
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
Matematika je exaktní věda. Pracuje s pojmy, které si sama definuje. Aby nám vypovídala něco o realitě, musíme si realitu namodelovat. Pokud by modelem jednoho bílku bylo číslo 1, modelem žloutku číslo 1 a modelem vajíčka číslo 1, pak platí žloutek=vajíčko, žloutek+bílek=dvě vajíčka, bílek+vajíčko=2 žloutky ... a spousta dalších nesmyslů. Abychom se jich zbavili, nemůžeme "ohnout" matematiku aby platilo 1+1=1, musíme vyměnit model. Žloutek namodelujeme jako X žlutých atomů, bílek jako Y bílých a vajíčko je X žlutých a Y bílých. A hurá, sčítání v modelu odpovídá realitě.
Příkladem situace, kdy v matematice "1+1=1" je Banach-Tarskiho paradox: http://en.wikipedia.org/wiki/Banach-Tarski_paradox . Ale ten určitě není dobrým modelem pro vajíčko. To by si pak jeden koupil vajíčko, šikovně ho rozřezal, měl dvě, jedno prodal, druhé rozřezal ... a žil šťastně až do smrti.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#14 22. 05. 2009 13:57
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ 7867088:
Ano, přesně tak. Každé racionální číslo, které lze vyjádřit ve tvaru konečného desetinného rozvoje 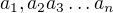 , lze vyjádřit také ve tvaru
, lze vyjádřit také ve tvaru 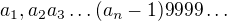 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#15 22. 05. 2009 15:43
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ 7867088:
Odpověď na první otázku: "Neznám!"
Odpověď na druhou otázku: "Ano!" - viz ↑ Pavel:
Offline
#16 22. 05. 2009 16:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Marian:
↑ 7867088: má asi na mysli toto.
Offline
#17 22. 05. 2009 16:20
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ BrozekP:↑ 7867088:
Radši bych akceptoval kvalitnější zdroj literatury, např. některý z pěti Ramanujanových zápisků (Ramanujan Notebooks I. - V., Lost Ramanujan Notebook) nebo Hardyho kniha Divergent series a podobné (které jste jistě znáte, že? :-)
Offline
#18 22. 05. 2009 16:34
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ BrozekP:
Pokud takto budeme definovat součet divergentních řad, tak v tom nevidím problém. Nicméně tento přístup nebude mít nic společného se s pojmem "součet nekonečné řady", tak jak ho známe, jenž je definován pomocí limity částečných součtů. Bude to naprosto nový pojem.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#19 22. 05. 2009 18:10 — Editoval Marian (22. 05. 2009 18:15)
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Pavel:
Omyl, pravdou je opak (ve většině případů). Metody sčítání divergentních nekonečných řad se zakládají na regulárních metodách sčítání (tzv. regular summability methods). Zhruba řečeno, pokud chceme jistou regulární metodou sčítat divergentní nekonečnou řadu, pak se součet nalezený pomocí nové metody nesmí lišit od klasického součtu ve smyslu Cauchyovy definice. Čili společného to má dost.
Mezi nejčastější metody sčitatelnosti se pak řadí Césarova, Nörlundova, Abelova, popř. velmi silná metoda Borelova. Existuje několik velice solidních klasických učebnic této teorie. Slovensky např. Tibor Šalát - Nekonečné rady (zcela závěrem knihy). Holendova kniha Řady toho moc nemá (uvádí pouze Töplitzovu větu). Doporučit mohu Hardyho knihu Divergent Series, popř. knihu od Jacoba Korevaara - Tauberian Theory. Pojem tauberiánských teorémů je však naznačen i v Šalátově knize.
Na druhou stranu - chtělo by se více podívat na to, co vlastně Motl popisuje (viz odkaz výše). Jestli metoda uvedená ve zmíněném odkazu je podle definice regulární metoda sčitatelnosti. Často tyto pojmy navíc souvisí s pojmem analytického prodloužení funkcí (v jeho případě patrně k výsledku dospěl pomocí úvahy o Riemannově funkci 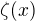 ).
).
Offline
#20 22. 05. 2009 18:39 — Editoval Pavel (22. 05. 2009 18:40)
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Marian:
Měl jsem na mysli to, že sečíst divergentní řadu pomocí regulárních metod (-1/9) je něco jiného než určit její součet pomocí limity částečných součtů (nekonečno). To je evidentní. V tomto symslu je určení součtu divergentní řady pomocí těchto metod nový pojem ve srovnání s určetním součtu divergentní řady pomocí částečných součtů. Nic víc, nic míň.
Nerozumím proto větě:
"...pokud chceme jistou regulární metodou sčítat divergentní nekonečnou řadu, pak se součet nalezený pomocí nové metody nesmí lišit od klasického součtu ve smyslu Cauchyovy definice..."
protože veškeré divergentní řady mají ve smyslu Cauchyovy definice součet roven plus (mínus) nekonečnu, nebo takovýto součet neexistuje.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#21 22. 05. 2009 18:53 — Editoval Marian (22. 05. 2009 18:55)
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
↑ Pavel:
Také té větě nerozumím. Když jsem odeslal příspěvek, to, co jsem tam měl chybělo. Tak jsem to v rychlosti dopisoval a cosi mi ulítlo. S tvým posledním příspěvkem souhlasím.
Nemohu však stále akceptovat tvou větu, na kterou narážím ve svém předchozím příspěvku, totiž
Nicméně tento přístup nebude mít nic společného se s pojmem "součet nekonečné řady", tak jak ho známe, jenž je definován pomocí limity částečných součtů.
Slovo nic má značit skutečně nic (často se s takovým slovem zbytečně plýtvá, možná podobně jako ve zdravotnictví s antibiotiky :). Jenže ta souvislost u regulárních metod sčitatelnosti nebo analytickým prodloužením funkcí s klasickými pojmy (u nekonečných řad tedy jejich součet ve smyslu Cauchyovy definice přes parciální součty) je evidentní. Totiž suma se u konvergentních řad (to je doplněné torzo věty, které nerozumíš - a já také ne po tvé připomínce - v mém předchozím příspěvku) se při použití regulérní metody musí rovnat sumě chápané jako limita parciálních součtů, což je totéž jak jsi před chvílí psal.
Ale to ty dobře víš. Tedy pouze to slovo "nic" ve mně probudilo jakýsi druh matematické nevole.
Offline
#22 25. 05. 2009 09:48 — Editoval Rumburak (25. 05. 2009 10:33)
Re: Zvlášnosti matematiky aneb 1 + 1 = 1
Pokusím se poněkud jinými slovy říci to, co vyjádřil Marian:
Chceme-li zavádět nějakou "novou" sčítací metodu, pak taková metoda by měla být rozšířením "klasické" sčítací metody
(v níž součet řady je definován jako limita posloupnosti částečných součtů).
Podrobněji: Označíme-li  limitu posloupnosti částečných součtů posloupnosti
limitu posloupnosti částečných součtů posloupnosti 
a  součet řady sestavené z téže posloupnosti vypočítaný podle "nové" sčítací metody, pak by měla platit následující věta:
součet řady sestavené z téže posloupnosti vypočítaný podle "nové" sčítací metody, pak by měla platit následující věta:
"Jeli  posloupnost, pro niž existuje
posloupnost, pro niž existuje  , pak existuje i
, pak existuje i  a
a 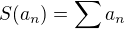 ."
."
EDIT. Obvykle též požadujeme, aby množina posloupností  sčítatelných podle nové definice ke konečnému "součtu"
sčítatelných podle nové definice ke konečnému "součtu" 
byla lineárním prostorem, na němž funkcionál S je lineární formou.
Offline
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Zvlášnosti matematiky aneb 1 + 1 = 1 (TOTO TÉMA JE VYŘEŠENÉ)