Matematické Fórum

O.o · 08. 01. 2009 21:39 — Editoval O.o (08. 01. 2009 21:43)

Ahoj .),

mám menší problém. Kamarádka potřebovala pomoc s něčím ke zkoušce a zasekli jsme se na jednom příkladě.

Jde o výpočet arctg(1,08) pomocí taylora druhého stupně.

Postupoval jsem takto:

$arctg(1,08) = ? \nl f(x) = arctg(x) \nl x_0 = 0 \ \Rightarrow \ f(x_0)=0 \nl$

Taylora máme jako:

$T_n(x, x_0) = f(x_0) + \sum_{k=1}^{n}{\frac{f^k(x_0)}{k!}(x-x_0)^k}$

Tak jsem začal řešit derivace (první dvě - taylor má být druhého stupně):

$f'(x) = \frac{1}{1+x^2} \ \rightarrow \ f'(x_0)=1 \nl f''(x) = \frac{-2x}{(1+x^2)^2} \ \rightarrow \ f''(x_0) = 0$

Ty derivace se mi už nějak nelíbí, možná jsem měl volti jiné x_0 (volil jsem sám, protože tam hodnotu arctg znám).

Dal jsem se tedy na dosazování do té formule co jsem psal výše (pokud není dobře, tak se omlouvám, sumační znak jsem dosazoval později, tak mi možná něco ujelo):

$T_2(x, 0) = f(0) + \sum_{k=1}^{2}{\frac{f^k(0)}{k!}(x-0)^k} = 0 + \frac{1}{1!}(x) + \frac{0}{2!}(x)^2 = x \nl T_2(1,08, 0) = 1,08 \nl arctg1,08 = 0,82384...$

Nějak se mi to prostě nezdá. Nepřipadá mi to správně. Mohl bych poprosit, kde jsem udělal chybu?

EDIT: $x_0$ si mohu volit jaké chci, nebo je pro to nějaké pravidlo?

kaja.marik · 08. 01. 2009 21:44

dal bych x_0=1

O.o · 08. 01. 2009 21:53 — Editoval O.o (08. 01. 2009 21:55)

↑ kaja.marik:

Díky za radu, to už jsem zkoušel také (je fakt, že spíš po paměti, protože dopsala propiska), ale stejně mi to nějak nevycházelo.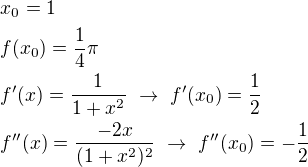

$x_0=1 \nl f(x_0) = \frac{1}{4}\pi \nl f'(x) = \frac{1}{1+x^2} \ \rightarrow \ f'(x_0)=\frac{1}{2} \nl f''(x) = \frac{-2x}{(1+x^2)^2} \ \rightarrow \ f''(x_0) = -\frac{1}{2}$

Potom dosadím a dostanu se k:

$T_2(x, 1) = f(1) + \sum_{k=1}^{2}{\frac{f^k(1)}{k!}(x-1)^k} = \frac{1}{4}\pi + \frac{\frac{1}{2}}{1!}(x-1) + \frac{-\frac{1}{2}}{2!}(x-1)^2 \nl T_2(1,08, 1) = 0,823798163... \nl$

Opravdu to vychází lépe, asi jsem to původně špatně dosadil, ale čistě ze zvědavosti, je nějaký tip na volení počátečního x? Nám říkal cvičící, abychom si volili bod, kde tu funkci známe (abych dal hodnotu z hlavy), abych řekl pravdu. Hraje v přesnosti výsledku asi roli i to, jak je x_0 vzdálené od hodnoty, pro kterou máme funkci přibližně zjistit? Jen mne to tak napadlo, že jednotka je k 1,08 blíže než 0 .)

PS: Ještě jednou díky..

kaja.marik · 08. 01. 2009 22:50

O.o napsal(a):
Hraje v přesnosti výsledku asi roli i to, jak je x_0 vzdálené od hodnoty, pro kterou máme funkci přibližně zjistit? Jen mne to tak napadlo, že jednotka je k 1,08 blíže než 0 .)

Urcite, doporucuji
* zagooglit na tema lagrangeuv tvar zbytku
* uvedomit si, ze tecna (lienarni lagrangeuv polynom) se obecne primyka k funkci jenom v okoli bodu dotyku. Dal uz muzou byt hodne daleko
* prohlednout si obrazky http://www.math.muni.cz/~plch/nkpm/nradanm6.pdf - cim vetis stupen polynomu, tim dyl se ten polynom mota nekde kolem aproximovane funkce. Nakonec se ale stejne vetsinou odkloni.

Videl jsem ve vedlejsich vlaknech neco o zkousce z biologie. Tak jak to dopalo? :)

O.o · 09. 01. 2009 09:03 — Editoval O.o (09. 01. 2009 09:08)

↑ kaja.marik:

Díky moc, určitě si to projdu, jak to jen půjde .)

No, zkouškou jsem prošel, sice hrůzně oznámkován, ale byl to druhý pokus, tak jsem nadšený, že jsem se téhle nepěkné zkoušky zbavil, příští týden už je matika a pak chemie (Ouch!) .)

EDIT: ttopi gratuluji, sice nemám tušení o čem ten předmět může být, ale zní to zajímavě, vkaždém případě ať se daří i nadále ;)

ttopi · 09. 01. 2009 09:07 — Editoval ttopi (09. 01. 2009 09:13)

↑ O.o:

Zdravím a gratuluji. Já absolvoval v úterý zkoušku z Algebry a Aritmetiky a byl jsem také úspěšný (otázky: 1)Cantorova konstrukce reálných čísel, 2)Barvení grafu).

Omlouvám se za OT :-)

kaja.marik · 09. 01. 2009 11:17

↑ O.o:
Tak to gratuluji.

Jinak, ja jsem barveni grafu venoval vcerejsi i predvcerejsi odpoledne s malou dcerkou. Hlavni je, naucit se pekne drzet v ruce pastelku a pokud barvim vodovkama, tak nenadelat moc binec kolem sebe :)

O.o · 09. 01. 2009 11:34

↑ kaja.marik:

Já když vezmu do ruky cokoli co píše, kreslí (...), tak nejvíce barvy zůstane na mne .)

PS: Ještě jednou ttopi gratuluji .)

ttopi · 09. 01. 2009 14:10

↑ kaja.marik:
Takže dcerka bude mít jednou z Algebry a Aritmetiky za 1 :-))

↑ O.o:
No o čem je ten předmět, to by měl říkat název, ne?
Konkrétně tady je sylabus tohoto kurzu pro představu

Sylabus I:Zavedení přirozených čísel (Peanova aritmetika). Konstrukce celých a racionálních čísel pomocí pojmu podílové grupy a tělesa. Otázka konstrukce reálných čísel. Čísla komplexní. Pojem algebraické řešitelnosti algebraických rovnic. Některé numerické metody řešení.

Sylabus II: Základy teorie množin (pojem konečné množiny, otázka sestrojení přirozených čísel v teorii množin, kardinality číselných struktur). Základy teorie svazů, aplikace svazů a Booleových algeber. Základní pojmy teorie grafů, aplikace.

O.o · 09. 01. 2009 14:25

↑ ttopi:

Nezapomeň, že nejsem matematik, název předmětu je pěkný, ale musel bych to hledat po netu a to mi lenost nedovoluje .). Určitě věřím, že je to zajímavý předmět a tebe určitě hodně baví :o)

ttopi · 09. 01. 2009 14:37

↑ O.o:
Ne, nebaví, z jednoho prostého důvodu.
Máme na to (měli jsme, už mam za sebou obě části) sice výborného matematika a odborníka prof. RNDr. Ing. Petr Němec DrSc. ale jak už to tak bývá, čím více tomu ten učitel rozumí, tím méně to umí podat. Takže ty hodiny byly celkem nudné. On furt psal nějaké důkazy, doslova se v tom vyžíval, všechno pro něj bylo jasné, takže se ani nezastavoval, navíc 3 hodiny v kuse, to je celkem lahůdka. Kolikrát jsem tam byl i sám :-)

O.o · 09. 01. 2009 15:23

↑ ttopi:

Myslím, že tak to chodí všude, záleží jen na tom, koho "chytneš", u nás zase na přednášky biologie chodilo už v polovině semestru, tak deset lidí a na prvé nás bylo přes dvěstě .)

Řekl bych, že ten OT bychom měli nějak ukončit nebo se to tu moc rozroste .)

ttopi · 09. 01. 2009 15:33

Souhlas, budiž OT ukončen :-)

Matematické Fórum

#1 08. 01. 2009 21:39 — Editoval O.o (08. 01. 2009 21:43)

Taylorův polynom

#2 08. 01. 2009 21:44

Re: Taylorův polynom

#3 08. 01. 2009 21:53 — Editoval O.o (08. 01. 2009 21:55)

Re: Taylorův polynom

#4 08. 01. 2009 22:50

Re: Taylorův polynom

O.o napsal(a):

#5 09. 01. 2009 09:03 — Editoval O.o (09. 01. 2009 09:08)

Re: Taylorův polynom

#6 09. 01. 2009 09:07 — Editoval ttopi (09. 01. 2009 09:13)

Re: Taylorův polynom

#7 09. 01. 2009 11:17

Re: Taylorův polynom

#8 09. 01. 2009 11:34

Re: Taylorův polynom

#9 09. 01. 2009 14:10

Re: Taylorův polynom

#10 09. 01. 2009 14:25

Re: Taylorův polynom

#11 09. 01. 2009 14:37

Re: Taylorův polynom

#12 09. 01. 2009 15:23

Re: Taylorův polynom

#13 09. 01. 2009 15:33

Re: Taylorův polynom

Zápatí