Matematické Fórum

Brano · 31. 03. 2013 16:39

Pri citani jedneho clanku ma napadlo takato uloha/otazka (ja odpoved neviem).

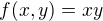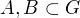Nech G je topologicka grupa - t.j. grupa na ktorej mame taku topologiu, ze $f(x,y)=xy$ a $g(x)=x^{-1}$ su spojite funkcie. Pre $A,B\subset G$ definujme $AB=\{xy\in G;x\in A;y\in B\}$ .

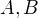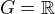Je zname, ze ak $A,B$ su uzavrete, tak $AB$ nemusi byt uzavreta - priklad $G=\mathbb{R}$ (operacia je scitanie), 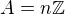$A=n\mathbb{Z}$ a $B=n\pi\mathbb{Z}$ potom $AB$ je husta a vlastna podmnozina $\mathbb{R}$ cize nie je uzavreta.

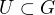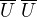Moja otazka je: Dokazte, alebo najdite kontrapriklad, ze ak $U\subset G$ je otvorena a $\overline{U}$ oznacuje uzaver $U$ potom $\overline{U}\;\overline{U}$ je uzavreta.

kompik · 03. 04. 2013 20:04 — Editoval kompik (03. 04. 2013 20:51)

V grupe $(\mathbb R^2,+)$ zober $U=\{(x,y)\in\mathbb R^2; y>1/{|x|}\}$ .
Vychádza mi $(\overline U)^2=\{(x,y)\in\mathbb R^2; y>0\}$ .
(Dúfam, že som tam nič neprehliadol.)

Pridám ešte poznámku, že ak chceme nájsť takýto príklad, tak množina $\overline U$ nemôže byť kompaktná. (A pri hľadaní kontrapríkladu môže pomôcť pozrieť sa na to, ako ide dôkaz v kompaktnom prípade.)
MSE: Product of compact and closed in topological group is closed

Brano · 03. 04. 2013 20:45

↑ kompik:
Ahoj, o tom odkaze viem, odtial som zobral to svoje $A,B$ . A co sa tyka tvojho prikladu ... co je $+$ ? Ak by to bolo scitanie po zlozkach, tak by bolo $\overline{U}\;\overline{U}=\overline{U}$ nie?

kompik · 03. 04. 2013 20:52 — Editoval kompik (03. 04. 2013 20:54)

Brano napsal(a):
↑ kompik:
Ahoj, o tom odkaze viem, odtial som zobral to svoje $A,B$ . A co sa tyka tvojho prikladu ... co je $+$ ? Ak by to bolo scitanie po zlozkach, tak by bolo $\overline{U}\;\overline{U}=\overline{U}$ nie?

Mal som na mysli obvyklé sčitovanie (po súradniciach), ale mal som tam preklep v definícii $U$ ; mal som napísať $y>1/{|x|}$ a napísal som $y>1{|x|}$ .

To je trest za to, že špekulujem, či lepšie vyzerá 1/|x| alebo \frac1{|x|} a potom nenapíšem ani jedno poriadne.

Brano · 03. 04. 2013 21:04

↑ kompik:
dakujem teraz je to ok - a ved som sa aj divil, ze preco pises tak divne, ze $y>1{|x|}$

Matematické Fórum

#1 31. 03. 2013 16:39

topologicke grupy

#2 03. 04. 2013 20:04 — Editoval kompik (03. 04. 2013 20:51)

Re: topologicke grupy

#3 03. 04. 2013 20:45

Re: topologicke grupy

#4 03. 04. 2013 20:52 — Editoval kompik (03. 04. 2013 20:54)

Re: topologicke grupy

Brano napsal(a):

#5 03. 04. 2013 21:04

Re: topologicke grupy

Zápatí