Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 04. 2013 11:10 — Editoval Moabiter (06. 04. 2013 12:36)
Re: Kolmý průmět vektoru
Tuhle část algebry už jsem chvíli nedělal, ale co udělat pomocí skalárního součinu projekci na každy z vektorů toho prostoru a pak je sečíst dohromady?
edit:
Tenhle postup by fungoval jenom v orthogonální bázi.
Bylo by tedy potřeba bázi W orthogonalizovat a hledat projekci v té nové orthogonální bázi (která generuje ten samý prostor, a proto budou obě projekce stejné).
Offline
#3 06. 04. 2013 12:13
Re: Kolmý průmět vektoru
↑ miso_svk:
Nejdřív by bylo třeba ověřit, že vektory 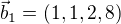 ,
,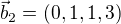 ,
, 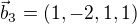 jsou lineárně nezávislé, takže dimenze W je 3 (to asi je).
jsou lineárně nezávislé, takže dimenze W je 3 (to asi je).
Pak je třeba kromě hledaného průmětu 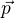 pracovat i s komponentou
pracovat i s komponentou  . Pro tyto vektory platí:
. Pro tyto vektory platí: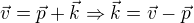 (1)
(1)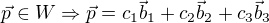 (2)
(2) (3)
(3)
Jestliže za  dosadíme z (1) do (3), dostaneme:
dosadíme z (1) do (3), dostaneme: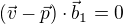
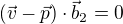
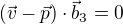
Za 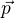 dosadíme ze (2)
dosadíme ze (2)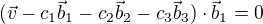
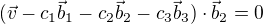
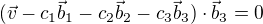
Je to soustava tří lineárních rovnic pro neznámé c_1;c_2;c_3, které po dosazení do (2) určí hledaný průmět.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#4 06. 04. 2013 12:39
Re: Kolmý průmět vektoru
↑ martisek: Hezký postup, fungoval by i ten můj tak jak jsem ho napsal?
Offline
#5 06. 04. 2013 13:27
Re: Kolmý průmět vektoru
↑ Moabiter:
Obávám se, že ne. Získali bychom projekce do jednotlivých vektorů, ale kdybychom je sečetli, nebyla by to ani projekce do vektorů, ani do toho W. Možno si to načrtnout pro dvojrozměrné W.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
