Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 04. 2013 00:41
Rovnice v oboru C
Ahoj, ještě bych se potřeboval poradit se správným postupem.
Opět mám řešit v  rovnici:
rovnici:
Opět uvažuji  .
.
Zase si rozdělím rovnici na imaginární a reálnou část.
imaginární 
reálná 
Tedy 
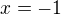
Je to tak správně? Já tam asi úplně moc chybu nevidím, nicméně výsledek má být  .
.
Offline
- (téma jako vyřešené označil(a) bejf)

 tam má správně být
tam má správně být 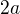 .
.