Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 04. 2013 21:07 — Editoval wolfito (09. 04. 2013 21:14)
Goniometrická rovnice
Zdravím,
Potřebuji pomoct s jednou rovnici. Spiš s postupem.
udělal jsem si substituci: 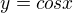
y mě vyšlo 
Ale nevím jak dal. Nebo jestli dělam dobře.
EDIT: - měl jsem ji špatně. Možna je ted dobře
- měl jsem ji špatně. Možna je ted dobře
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
- (téma jako vyřešené označil(a) wolfito)
#2 09. 04. 2013 21:22
Re: Goniometrická rovnice
↑ wolfito:
Pokud použiješ tu substituci, tak se počítá takto:
Vrátíš se k původní proměnné 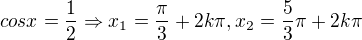
Offline

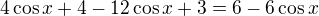

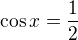 a výsledky. Nemusíš zavádět substituci, když to není potřeba
a výsledky. Nemusíš zavádět substituci, když to není potřeba