Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 14. 04. 2013 21:24 — Editoval elypsa (14. 04. 2013 21:24)
Re: Limita
Potom teda.![kopírovat do textarea $\lim_{x\to0+}\sqrt[3]{x}\cdot \ln x=0\cdot-\infty $](/mathtex/67/672aa2c9d2acea379aa11ed24aeeb466.gif)
Což se po úpravě dá vypočítat přes LH.![kopírovat do textarea $\lim_{x\to0+}\sqrt[3]{x}\cdot \ln x=\lim_{x\to0+}\frac{lnx}{\frac{1}{\sqrt[3]{x}}}=\lim_{x\to0+}\frac{\frac{1}{x}}{(x^{\frac{-1}{3}})'} \\=\lim_{x\to0+}\frac{\frac{1}{x}}{\frac{-1}{3}x^{\frac{-4}{3}}}=\lim_{x\to0+}\frac{1}{x}\cdot(-\frac{3\cdot\sqrt[3]{x^4}}{1})=\\=\lim_{x\to0+}(-\frac{3\cdot\sqrt[3]{x^4}}{x})="\frac{0}{0}"$](/mathtex/b2/b2644f496dc8370ae0f1a95d66d7b5ae.gif)
Opět použiješ LH zderivuješ čitatel a jmenovatel a mělo by vyjít http://www.wolframalpha.com/input/?i=li … from+right
Zvládneš?
Snad jsem se někde neupsal a nepřepočítal.
Baf!
Offline
#6 14. 04. 2013 21:44
Re: Limita
Můžu se jen tak zeptat...
Kdybych za x dosadil dejme tomu  opravdu malé číslo.
opravdu malé číslo.
Tak dostanu neuvěřitelně obrovské záporné číslo díky logaritmu krát malinké kldné číslo díky té odmocnině. Takže bych se dostal někam úplně do neuvěřitelně obrovskejch čísel. A až když tam dosadím nulu, tak to tam zaprvý není definovaný a za druhý to bude teoreticky nula až když tam dosadíte nulu. A není limita nahodou okolí bodu? když jdu k nule zprava tak přece jdu pořád do větších záporných čísel, a až na tý nule to skočí nahoru. Nemělo by to bejt tím pádem -nekonečno?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 14. 04. 2013 22:59
Re: Limita
↑ honzicek:
Abych řekl pravdu, tak radši neodpovím, protože prvně si nejsem jist zda tě plně chápu a pokud to teda chápu tak jak to chápu (:D), tak se bojím odpovědět, abych neřekl nějakou pitomost.. Tak snad někdo jiný :)
↑ Freedy:
Ahoj :)
Zkus si dosazovat do kalkulačky, uvidíš, že se to bude pomalu blížit k 0. Respektive tvé "neuvěřitelně obrovské záporné číslo díky logaritmu krát malinké kldné číslo díky té odmocnině" by mělo klesat k 0. No snad jsem se s odpovědí trefil :) popravdě nejsem nějaký mistr v limitách na tož abych se tu pouštěl do teorií O:-)...
Baf!
Offline
#10 15. 04. 2013 00:50 — Editoval found (15. 04. 2013 00:52) Příspěvek uživatele found byl skryt uživatelem found. Důvod: Nekonstruktivní postup.
#11 15. 04. 2013 10:39 — Editoval found (15. 04. 2013 14:43)
Re: Limita
↑ Freedy:
Ještě mě napadlo, že bych ti mohl odpovědět na tohle, co's psal.
Tvoje x je skutečně velice malé číslo. Z průběhu logaritmu dostaneme skutečně velice obrovské záporné číslo.
Nesmíme si však plést pojmy s dojmy. Když se bavíme o "malém" a "velkém" číslu, vlastně se bavíme o jeho velikosti, to jest absolutní hodnotě. Kupříkladu nejmenší číslo, kterého lze dosáhnout je  . To je v absolutní hodnotě ale zase největší číslo
. To je v absolutní hodnotě ale zase největší číslo  . A dosáhnout je myšleno čistě dosáhnout pomocí limity.
. A dosáhnout je myšleno čistě dosáhnout pomocí limity.
Tak a teď k tomu zbytku. Takže už víme, že kdybychom limitu roztrhli, dostlai bychom 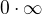 , což jak říkáš, je nedefinované - a přesně proto to takhle udělat NEMŮŽEME! Přesně jak píšeš, jde o okolí bodu, ne o žádný bod 0, v němž limitu zprava děláš. V samotné definici limity bod 0 vůbec nebude vystupovat. Zkoumáme, jak se funkce chová na okolí. Už jsme si ale ukázali, že na okolí jde jedna z funkcí k nule a druhá k mínus nekonečnu. A přesně z nedefinovatelnosti tohoto výrazu nemůžeme použít větu o aritmetice limit (totiž že limita součinu funkcí je součin limit těchto funkcí).
, což jak říkáš, je nedefinované - a přesně proto to takhle udělat NEMŮŽEME! Přesně jak píšeš, jde o okolí bodu, ne o žádný bod 0, v němž limitu zprava děláš. V samotné definici limity bod 0 vůbec nebude vystupovat. Zkoumáme, jak se funkce chová na okolí. Už jsme si ale ukázali, že na okolí jde jedna z funkcí k nule a druhá k mínus nekonečnu. A přesně z nedefinovatelnosti tohoto výrazu nemůžeme použít větu o aritmetice limit (totiž že limita součinu funkcí je součin limit těchto funkcí).
Kdybys chtěl nějaký komplexnější výklad limit apod., asi bych ti doporučil, aby sis našel nějaká skripta pro vysokoškoláky, nějaké úvody do studia diferenciálního počtu funkce jedné proměnné. Doporučil bych ti asi knihu od pana Kopáčka. Jmenuje se to nějak "Matematická analýza nejen pro fyziky I" nebo tak.
S pozdravem
J.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#13 15. 04. 2013 14:42
Re: Limita
↑ Jenda358:
Jéje, no to jsem tedy pěkně zkazil. :) Tak se omlouvám za desinformaci z mé strany, očividně jsem zapomněl na posunutí, kterého se dopustím. :(
Tak jako tak děkuji za upozornění.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
![kopírovat do textarea $\lim_{x\to0+}\sqrt[3]{x}\cdot \ln x$](/mathtex/48/4887d8344b1e0bf43531ed9e91e5f04a.gif)

![kopírovat do textarea $\cdots=\lim -\frac{3\sqrt[3]{x^4}}{x}=\lim-3x^{1/3}=0$](/mathtex/e0/e08d050c6ad9de3947a8a526f4d6963b.gif)
 .
. .
.