Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 01. 2009 11:35 — Editoval musixx (14. 01. 2009 11:44)
Re: Limita fce
↑ Frantik88: Kdyz argument logaritmu posunu o 1, nic se limitne nestane, takze z toho je videt, ze limita bude 0.
Chces-li to jinak, tak pis misto  funkci
funkci 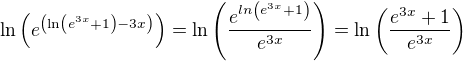 . Argument logaritmu jde k 1, tedy logaritmus sam k nule.
. Argument logaritmu jde k 1, tedy logaritmus sam k nule.
Offline
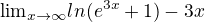


 . Ale jinou cestu jsem tez doplnil vyse.
. Ale jinou cestu jsem tez doplnil vyse.