Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » modus všeobecného rozdelenia (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 04. 2013 19:21
modus všeobecného rozdelenia
Čaute je nejako definovaný modus pre všeobecné rozdelenia všade sa píše len pre diskrétne a spojité ale je nejako definovaný modus napr. pre náhodnú premennú s distribučnou funkciou, ktorá je súčtom diskrétnej a absolútne spojitej prípadne dokonca pre singulárne rozdelenie?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#4 21. 04. 2013 23:19 — Editoval Brano (21. 04. 2013 23:20)
Re: modus všeobecného rozdelenia
↑ martisek:
no ved to je v podstate asi predmet jarrovej otazky. raz sa to definuje ako maximum hostoty voci lebesgueovej miere v pripade spojitych a v pripade diskretnych rozdeleni sa berie hostota vzhladom na rovnomernu mieru na diskretnej podmnozine  a pyta sa ci sa to da zjednotit; ak som to teda spravne pochopil
a pyta sa ci sa to da zjednotit; ak som to teda spravne pochopil
Offline
#6 22. 04. 2013 00:23
Re: modus všeobecného rozdelenia
↑ jarrro:
to myslim, ze neexistuje skus uvazit toto - t.j. dokaz alebo vyvrat (pre mna je moc neskoro aby som sa seriozne zamyslel)
Nech  je nejaka distribucna funkcia a kedze ta ma iba spocitatelne vela skokov, tak musi existovat
je nejaka distribucna funkcia a kedze ta ma iba spocitatelne vela skokov, tak musi existovat  t.z. taky, ze
t.z. taky, ze  je spojita v
je spojita v  a potom
a potom
nie je absolutne spojita voci  - t.j. nema hustotu.
- t.j. nema hustotu.
Offline
#7 22. 04. 2013 10:14
Re: modus všeobecného rozdelenia
↑ Brano:ďakujem pekne ešte by som sa opýtal, že potom podľa tej tvojej konštrukcie by singulárna náhodná premenná (so spojitou ale nie absolútne spojitou distribučnou funkciou) mala každú hodnotu za modus je to tak? (viem, že aj pekné napr. rovnomerne rozdelené náhodné premenné majú každú hodnotu s kladnou pravdepodobnosťou nadobudnutia za modus)
MATH IS THE BEST!!!
Offline
#8 22. 04. 2013 10:17
Re: modus všeobecného rozdelenia
Tak ja by som tu neexistenciu dokazal takto.
Nech 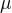 je miera na borelovskych na
je miera na borelovskych na  a nech
a nech  je pravdepodobnost absolutne spojita voci
je pravdepodobnost absolutne spojita voci 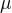 t.j. ma hustotu
t.j. ma hustotu  t.z.
t.z.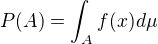
Mozme si vsimnut, ze potom musi nutne platit
1)  potom
potom 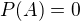
2)  a
a 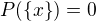 potom
potom 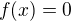
Teraz nech 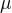 je taka, ze lubovolna
je taka, ze lubovolna  ma voci nej hustotu - ukazeme, ze je to sporne.
ma voci nej hustotu - ukazeme, ze je to sporne.
Ak by existoval  taky, ze
taky, ze  potom take
potom take  ktore splna
ktore splna  nema (podla 1)) hustotu voci
nema (podla 1)) hustotu voci 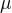 . Teda pre vsetky
. Teda pre vsetky 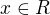 musi byt
musi byt  . (To je inak dost nezaujimava miera) Uvazujme teraz lubovolnu
. (To je inak dost nezaujimava miera) Uvazujme teraz lubovolnu  absolutne spojitu voci Lebesgueovej miere (napr. normalne rozdelenie) potom pre lubovolne
absolutne spojitu voci Lebesgueovej miere (napr. normalne rozdelenie) potom pre lubovolne 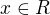 plati
plati 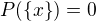 a teda
a teda 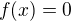 cize dostavame
cize dostavame  co je spor.
co je spor.
Offline
#10 22. 04. 2013 12:37 — Editoval jarrro (22. 04. 2013 12:45)
Re: modus všeobecného rozdelenia
↑ Brano:singulárna n. p. je n.p., ktorej distribučná funkcia je spojitá, ale nie absolútne spojitá napr. Cantorove schody
resp distribučná funkcia je singulárna
MATH IS THE BEST!!!
Offline
#11 22. 04. 2013 12:53
Re: modus všeobecného rozdelenia
↑ jarrro:
to znamena, ze pre singularnu je mimo mnoziny miery nula derivacia 0 cize nemoze tam byt modus podla toho navrhu co som pisal, ale asi teda moze byt, ze by modusov bolo nespocitatelne vela, ale ostava otazka, ci by ich mnozina mohla mat mieru vacsiu ako 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » modus všeobecného rozdelenia (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $A(x)=\lim_{\epsilon\to0^+}\frac{F(x+\epsilon)-F(x)}{\epsilon}\in[0,\infty]$](/mathtex/07/07403a5b03f6b3834ef005b75358e1be.gif)
![kopírovat do textarea $B(x)=\lim_{\epsilon\to0^+}F(x+\epsilon)-F(x)\in[0,1]$](/mathtex/ac/ac738e7069d05794db7b97d898fe97d8.gif)
 potom
potom