Matematické Fórum

bejf · 26. 04. 2013 12:32

Ahoj. Chtěl bych se jen poradit s jedním příkladem z posloupností.

Posloupnost $(a_{n})^{\infty}_{n=1}$ je určena rekurentně takto: $a_{1}=0; a_{n+1}=a_{n}+2n+1, n\in N$ (pro každé n z N).
Dokažte (matematickou indukcí), že její n-tý člen lze vyjádřit vzorcem $a_{n}=n^2-1$ .

To jsem spočítal. Vzal jsem 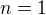$n=1$ a dosadil do vzorce pro n-tý člen a zjistil, že pro 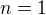$n=1$ je vztah splněn.
Pak jsem zjišťoval, jestli je také splněn pro $a_{n+1}$
$a_{n+1}=(n+1)^2-1=n^2+2n+1-1=(n^2-1)+2n+1=a_{n}+2n+1$ .

To by snad bylo všechno. Ale o co mi jde je, že nejsem schopen z toho rekurentního zadání dostat ten vzorec pro n-tý člen. :D

Zkouším:
Vypočítám nejprve třeba první tři členy a $a_{n-1},a_{n}$
$a_{1}=0, \nl a_{2}=0+2n+1=3, (n=1) \nl a_{3}=3+2n+1=8, (n=2)\nl \ldots \nl a_{n-1}=a_{n-2}+2(n-2)+1, (n=n-2) \nl a_{n}=a_{n-1}+2(n-1)+1, (n=n-1)$ Ty závorky jsou tam jen ilustrativní, aby bylo vidět, co se dosazuje za n.

Pak dostanu rovnici:
$a_{2}+a_{3}+\ldots +a_{n-1}+a_{n}=a_{1}+2n+1+a_{2}+2n+1+\ldots +a_{n-2}+2(n-2)+1+a_{n-1}+2(n-1)+1$
No a teď nevím jestli to mám vůbec dobře, a pokud ano, tak jak z toho nějak šikovně dostat ten vzorec pro n-tý člen. Asi mě tam mate to, že je tam navíc 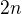$2n$ , tak právě nevím jak dál. Děkuji za rady.

nejsem_tonda · 26. 04. 2013 13:13

Tvuj postup v podstate vede na rovnost (po odecteni tech acek, ktere jsou stejne)
$a_n=3+5+7+9+\dots+(2n-1)$
coz se da secist jako aritmeticka rada, cimz dostaneme $a_n=n^2-1$ .

Taky se to da secist trikem, kteremu se nekdy rika teleskopicka suma. Kdyz si clovek uvedomi, ze
$2n+1=(n+1)^2-n^2$ ,
tak vlastne dostane
$a_n=(2^2-1^2)+(3^2-2^2)+(4^2-3^2)+(5^2-4^2)+\dots+(n^2-(n-1)^2)=n^2-1$

Jinak co se tyka obecne prevodu rekurentniho vztahu na explictni vyjadreni, tak to je tezky problem. Umi se to napr. pro linearni homogenni rekurence, vice na wikipedii.

bejf · 26. 04. 2013 13:19

↑ nejsem_tonda:
Aha, no tak to je koukám docela slušnej oříšek. Díky. :)

Matematické Fórum

#1 26. 04. 2013 12:32

Posloupnost

#2 26. 04. 2013 13:13

Re: Posloupnost

#3 26. 04. 2013 13:19

Re: Posloupnost

Zápatí