Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 04. 2013 14:17
Pád Měsíce k Zemi
Zdravim vsetkych,
zaujma ma ako sa da vypocitat doba padu Mesiaca k Zemi ak by na Mesiac neposobila odstrediva sila.
(vzhladom na vzdialenost Mesiaca od Zeme by som to chcel vediet aj so zohladnenim rychlosti svetla)
Dakujem za akekolvek rady
Offline
#2 27. 04. 2013 22:07
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Re: Pád Měsíce k Zemi
Musíš vediet veľkosť gravitačnej sily Zeme vo vzdialenosti mesiaca, taktiež veľkosť gravitačnej sily Mesiaca vo vzdialenosti Zeme a hmotnosť Mesiaca.Predpokladaj, že Zem je "ukotvená" a nehýbe sa, bude sa ti tak ľahšie počítať a je to v podstate jedno. Ja osobne by som si vytvoril graf kde by som na osi y mal gravitačnú silu Zeme a Mesiaca a na osi x ich vzdialenost.
F = sila, ktorou na seba pôsobia Mesiac a Zem
m = hmotnosť Mesiaca
a = zrýchlenie Mesiaca
F / m = a
Z grafu by som vytvoril nový graf, kde na osi y by som mal vzdialenosť a na osi x zrýchlenie. Potom by som vypočítal priemerne zrýchlenie a vypočítal čas "voľného pádu".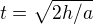
Je možné, že v tom mám chybu a neviem ako si to myslel s tou rýchlosťou svetla a taktiež neviem na čo to potrebuješ, čiže neviem ako veľmi presné to chceš. Dúfam, že som aspoň trochu pomohol.
Offline
#3 28. 04. 2013 10:00
Re: Pád Měsíce k Zemi
↑ Aikido21:
Ahoj,
za mě asi takto - na vzdálenosti celé Sluneční soustavy se vůbec opravy obecné teorie relativity uvažovat nemusejí (mimo nějaké stáčení dráhy Merkuru). Jak náš přednášející rád několikrát zmínil (a napsal i do skript), cesta na Měsíc se počítala dle klasické mechaniky.
Nicméně, záleží teď taky na tom, jak moc složitě chceš úlohu pojmout. Víme, že všechny inerciální systémy zastávají stejné tvary fyzikálních zákonů. Takže místo oběžné dráhy okolo Slunce můžeme počítat v soustavě, ve které udává kolega Robert. Jestli ale chceš mít úlohu o něco složitější a být si jistý tím, že to tak je správně, můžeš započítávat i pohyb Země okolo Slunce.
Pokud tedy mluvíme o síle působící na Měsíc, asi se sotva budeme pohybovat v relativitě, kde je nám bohem tensor křivosti. Tak to tedy vezmeme z pohledu klasické mechaniky. Máme dva hmotné objekty, které se přitahují - samozřejmě každý je přitáhován druhým a tedy různě urychlovaný (síla působící na obě objekty je stejná, jejich hmotnost však nikoliv). Také je třeba zmínit, že uvažujeme pouze gravitační interakci (mám za to, že Měsíc je elektroneutrální, takže EM síly tam působit nebudou ani lokálně a jaderné síly se na takové vzdálenosti nemají šanci projevit).
Takže teď je asi zapotřebí spočítat gravitační sílu, která působí na oba dvě objekty a nechat je se k sobě přibližovat. Samozřejmě zde nastane problém v počítání dráhy, která se mezi danými objekty snižuje dle jakéhosi zváštního vzorce. Dle mého dobrý způsob by mohl být místo určování polohy Měsíce a Země najít polohu těžiště soustavy a vzájemnou polohu Měsíce a Země. Tedy
Je v tuhle chvíli úplně jedno, jestli 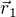 je poloha Země nebo Měsíce a stejně tak
je poloha Země nebo Měsíce a stejně tak 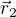 . Dál už by ale bylo třeba určovat Lagrangián soustavy a trošku víc si započítat.
. Dál už by ale bylo třeba určovat Lagrangián soustavy a trošku víc si započítat.
Dalším možným způsobem je hledání těžišťové vztažné soustavy a v této soustavě sledovat přibližování Měsíci i Země k těžišti. Musel bych si ale více promyslet, jak by tohle šlo udělat bez použití Lagrangeovy nebo Hamiltonovy mechaniky.
Další možností je udělat aproximaci pro hmotnost Země daleko větší než hmotnost Měsíce (to zde udělal kolega Robert - alespoň myslím). Co ale tak vím, tak ten rozdíl hmotností je pouze stonásobný, tak si nejsem jistý, jak moc přesné to řešení pak bude. Přijde mi ale, že se jedná o problém homogenity pole, protože kolega sice užívá něco jako průměrné zrychlení (tak asi předpokládá, že se bude měnit), ale ve finále používá pro výpočet času vzorec pro rovnoměrně zrychlený pohyb (tj. když se zrychlení nemění). A on je přecejenom rozdíl počítat s průměrným zrychlením a počítat s vývojem zrychlení po celou dobu. Možná bych se na jeho postup díval více jako na integrální záležitost, a potom bych s kolegou souhlasil - jenže zase nevím, nakolik moc znát integrály nebo zda vůbec víš, oč jde.
Inu, myslím, že pár návrhů, jak se na to podívat, tu máš, tak se s tím zkus poprat. Finálně bych doporučil jednu věc k tomu počítání. Najdi si vzájemnou vzdálenost těžišť Měsíce a Země ve chvíli, kdy do sebe objekty narazí (tj. součet poloměrů planet). Při počítání si pak uvědom, že počítáš, kdy se dostanou těžiště planet do této vzdálenosti, nikoliv kdy se jejich těžiště stanou jedním (tj. vzdálenost nejde do nuly, ale právě do součtu poloměrů).
S pozdravem
J.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 28. 04. 2013 11:58
Re: Pád Měsíce k Zemi
Dakujem obidvom za hodnotne prispevky najma "found", to s rychlostou svetla je moja chyba (je to blbost), nepotrebujem to ani z daleka tak presne...postacuje mi presnost na urovni jednoduchej mechaniky.
Vecer budem mat viac casu sa pozriet na to a vyskusam co sa podari vytvorit z postupu GeekRoberta.
Offline