Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 04. 2013 08:37 — Editoval Bati (27. 04. 2013 09:13)
Re: poloměr setrvačnosti
↑ Rufus:
Zdravím,
mezikruží samo o sobě nebude mít žádnou hmotnost, protože nemá žádný objem, takže je asi lepší si to představovat jako dutý válec s hodně malou výškou. To už lze najít na wikipedii, anebo jednoduše odvodit: Víme že obsah mezikruží je 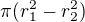 a hledáš takový poloměr
a hledáš takový poloměr  , abys jeho plochu rozdělil na stejně velké části:
, abys jeho plochu rozdělil na stejně velké části: 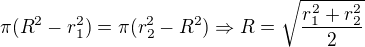 .
.
Offline

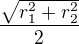 . Matematické zápisy jsou vždy jednoznačné, stačí je pozorně číst.
. Matematické zápisy jsou vždy jednoznačné, stačí je pozorně číst.