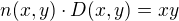Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 05. 2013 09:53
důkaz dělitelnosti
Ahoj, potřebovala bych pomoci se dvěmi příklady k maturitě.
1. Zadání: Dokažte, že součet čtverců dvou po sobě následujících přirozených čísel zmenšený o 1 je dělitelný čtyřmi.
Řešení: předpokládám, že součtem se myslí obsah. Konkrétně to tedy bude např: 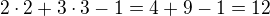 ... 12 je dělitelné 4mi.
... 12 je dělitelné 4mi.
Obecně: 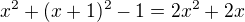 .. ale to mi asi k ničemu není, teoreticky to chápu, ale nedokážu dát přesný důkaz.
.. ale to mi asi k ničemu není, teoreticky to chápu, ale nedokážu dát přesný důkaz.
2.zadání: Jsou daná 2 přirozená čísla x,y. D(x,y)=6, n(x,y)=90. Určete je, víte-li, že x=30. (výsledek má vyjít 18). S tímto příkladem si neumím poradit, prosím o nějakou radu aspoň jak začít.
Offline
- (téma jako vyřešené označil(a) Nicky.)
#3 05. 05. 2013 11:26
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: důkaz dělitelnosti
↑ Nicky.:
2) Neni v tom nic vic, nez si rozmyslet, jak se z rozkladu na prvocisla pocita n(x,y) a D(x,y). Po chvilce rozmysleni se navic da prijit na vztah
Offline