Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 10. 05. 2013 18:27
Re: Tečná rovina a normála plochy
Ahoj. Plochu musíš najskôr parametrizovať. Potom parametrizáciu zderivuješ podľa prvého parametra, dostaneš nejaký vektor. Potom tú istú parametrizáciu zderuvuješ podľa druhého parametra a dostaneš druhý vektor.
Tieto vektory sú smerové vektory plochy a normálový vektor dostaneš ich vektorovým súčinom.
Offline
#3 10. 05. 2013 19:46
Re: Tečná rovina a normála plochy
Nebo můžeš postupovat následovně: Funkci si napiš ve tvaru F(x,y,z)=0 a vytvoř gradient této funkce, tzn. vektor prvních parciálních derivací funkce, podle všech proměnných (F'x, F'y, F'z), tento vektor je zároveň normálou plochy v jejím libovolném bodě.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#4 10. 05. 2013 20:04 — Editoval user (10. 05. 2013 20:05)
Re: Tečná rovina a normála plochy
Ahoj,
jen doplním, že parametrizaci už máš zadanou pomocí x a y. Formálně 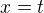 ,
, 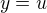 :
: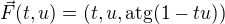 .
.
Další možnou představou je hledět na plochu jako na graf funkce, velikost parciální derivace v bodě mi udává směrnici tečny v daném bodě a směru parciální derivace.
Směrové vektory tečné roviny v bodě 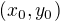 podle této úvahy jsou:
podle této úvahy jsou: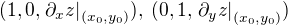
Offline
