Matematické Fórum

madeat · 18. 01. 2009 19:40

Dobrý večer mám problém s následujícím příkladem

Děkuji

Pavel Brožek · 18. 01. 2009 19:46

↑ madeat:

$\lim_{x\to0}\frac{\tan 8x}{x}=8\lim_{x\to0}\frac{\sin 8x}{8x}\cdot\frac{1}{\cos8x}=8\lim_{x\to0}\frac{\sin 8x}{8x}$

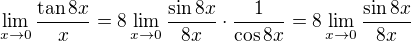
Dál substituce 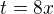$t=8x$ . Stačí takhle?

madeat · 18. 01. 2009 19:55

Stačí moc děkuji, ale měla bych keště jeden příklad jestli můžu..............

Pavel Brožek · 18. 01. 2009 19:58

↑ madeat:

Znáš limitu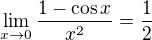

$\lim_{x\to0}\frac{1-\cos x}{x^2}=\frac12$ ,

umíš l'Hospitalovo pravidlo nebo znáš Taylorův rozvoj? (To jsou tři asi nejjednodušší možnosti jak vypočítat tuto limitu.)

Frantik88 · 18. 01. 2009 20:39

↑ BrozekP:
Ten první příklad jsem počítal zleva a zprava pro 0 bez substituce s pomocí lopitala a vyšlo mi 8, taky možnost ne?

Pavel Brožek · 18. 01. 2009 20:42

↑ Frantik88:

Taky možnost, ale proč počítat zvlášť zleva a zprava, když to jde rovnou?

Frantik88 · 18. 01. 2009 20:46

↑ BrozekP:
Máš pravdu, po dosazení nevyšlo 1/0, tudíž, retardace se opět projevila. =D

Matematické Fórum

#1 18. 01. 2009 19:40

Limity

#2 18. 01. 2009 19:46

Re: Limity

#3 18. 01. 2009 19:55

Re: Limity

#4 18. 01. 2009 19:58

Re: Limity

#5 18. 01. 2009 20:39

Re: Limity

#6 18. 01. 2009 20:42

Re: Limity

#7 18. 01. 2009 20:46

Re: Limity

Zápatí