Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 05. 2013 14:25
Konstrukcia grup
Dnes vam tu navrhujem toto cvicenie:
Najdite grupy, generovane dvomy roznymy prvkamy  a
a  takymy ze
takymy ze
a) 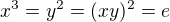
b) 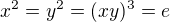
Poznamka:  je neutralny prvok kazdej grupy.
je neutralny prvok kazdej grupy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
- (téma jako vyřešené označil(a) byk7)
#2 12. 05. 2013 22:20
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Konstrukcia grup
↑ vanok:
Ahoj, znamená to, že x i y jsou generátory (tj. jak x, tak y generují grupu - a ta je tedy cyklická) a nebo, že je generátorem množina {x,y}? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#3 12. 05. 2013 23:03 — Editoval vanok (12. 05. 2013 23:22)
Re: Konstrukcia grup
Pozdravujem ↑ check_drummer:,
a) Taka grupa ma prvky ktore su konecne suciny x a y, take ze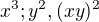 sa mozu nahradit z
sa mozu nahradit z  .
.
priklady: 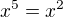
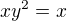
Da sa to vyjadrit aj takto:
Mozes povazovat, ze jej prvky su konecne slova napisane vdaka 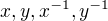 ktore sa daju zjednodusit podla vysie napisanych pravidiel.
ktore sa daju zjednodusit podla vysie napisanych pravidiel.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 05. 2013 22:55
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Konstrukcia grup
↑ vanok:
Ahoj, zkusím bod a):
díky součinům, které se rovnají identitě lze najít inverzní prvky k několika prvkům, a sice:
1. 
2. 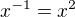
3. 
4. 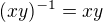
5. 
6. 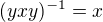
Pak porovnáním 1. a 5. máme
7. 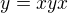
A porovnáním 3 a 6 máme
8. 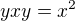
Díky 8. a vlastnostem x,y stačí uvažovat jen takové prvky, ve kterých se střídají xyxyxy... Každý jiný lze přepsat na tento tvar (počítaje v tento tvar i identitu).
Ovšem xyx lze zjednodušit na y a tedy lze rovněž předpokládat, že se v žádném prvku nevyskytuje součin xyx.
Když to shrneme, tak možné prvky jsou e,x,y,xy,yx,yxy.
Zbývá pak určit jen 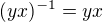 (plyne z 5,6 a ze 7). Pokud předpokládáme
(plyne z 5,6 a ze 7). Pokud předpokládáme 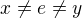 , pak žádné dva uvedené prvky se nerovnají. Tabulku násobení lze snadno odvodit z výše uvedených vztahů a zbývá ověřit, zda je tato operace asociativní (to jsem neprovedl).
, pak žádné dva uvedené prvky se nerovnají. Tabulku násobení lze snadno odvodit z výše uvedených vztahů a zbývá ověřit, zda je tato operace asociativní (to jsem neprovedl).
"Máte úhel beta." "No to nemám."
Offline
#5 15. 05. 2013 01:05 — Editoval vanok (15. 05. 2013 01:10)
Re: Konstrukcia grup
Pozdravujem ↑ check_drummer:,
Ano tvoja uvaha je dobra. A da sa doplnit na dokonaly dokaz.
Tu pridam, ako som uvazoval, ja.
Najprv predpokladam, ze ani  a ani
a ani  nie su
nie su  .
.
Zo zadania vieme, ze 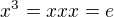
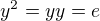

Z  odvodim
odvodim 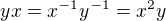
a potom 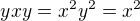 a tiez
a tiez 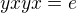
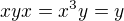
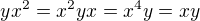
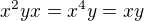
Toto zarucuje ze kazdy vyraz, sucin 4och prvkov sa da zjednodusit na vyraz, z najviac z 3my prvkamy, a nakoniec na jeden z 
Akoze, podla predpokladu 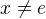 a
a 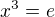 ,
,  je radu 3.
je radu 3. je radu 2. To znamena, ze rad tejto konecnej grupy je delitelny cislom 6.
je radu 2. To znamena, ze rad tejto konecnej grupy je delitelny cislom 6.
A z toho co je ukazane vysie jej rad je 6.
Akoze tato grupa nie je komutativna, tak je izomorfna z 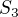 .
.
Co sa da detailne ukazat tak, ze x je isomorfne z cyklom (1;2;3) a y z tranpoziciou (1,2).
Poznamka: pripady kde 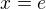 a
a 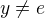
ako aj 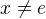 a
a 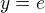 su jednoduche, tak ich necham pre citatelov.
su jednoduche, tak ich necham pre citatelov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 17. 05. 2013 14:36
Re: Konstrukcia grup
Navod na otazku b).
Pochopitelne, da sa pouzit taka ista metoda ako som pouzil vyssie.
Ale rychlejsieje vyuzit otazku a). Ako?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 18. 05. 2013 23:49
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Konstrukcia grup
↑ vanok:
Ahoj, položme x1:=xy, y1:=y a použijme na x1,y1 bod a). Lze snadno ukázat, že pak platí i 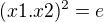 a pak tedy podle a) jsou prvky grupy e,x1,y1,x1.y1,y1.x1,y1.x1.y1 a po rozepsání pomocí x,y získáme prvky e,x,y,xy,yx,yxy (tedy stejné jako v případě a)).
a pak tedy podle a) jsou prvky grupy e,x1,y1,x1.y1,y1.x1,y1.x1.y1 a po rozepsání pomocí x,y získáme prvky e,x,y,xy,yx,yxy (tedy stejné jako v případě a)).
"Máte úhel beta." "No to nemám."
Offline
#8 19. 05. 2013 00:38
Re: Konstrukcia grup
↑ check_drummer:,
Ahoj, dobra praca.
Cim skor dam dalsie cvicenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
