Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 05. 2013 15:36
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Analyticka geometrie
Ahoj,
doucuju matiku, analyticku geometriu, ale nejak som sa zamotal, vedeli by ste mi pomoct?
priklad
Napiste rovnici primky, ktera prochazi bodem P[-2,5], a ma od bodu R[3,5] vzdalenost 
Vysledek ma vyjit, primky 

Delal jsem to podle tohto vlakna
http://forum.matweb.cz/viewtopic.php?id=61972
Ale nejak mi to nevyslo. Taky jsem zkousel si vyjadrit souradnice bodu
X, ktery by mel byt patou kolmice od primky k bodu R. S tim, ze vim ze a taky jsem si dopocetl z trojuhelniku XRP vzdalenost |XP|, co mi vyslo
a taky jsem si dopocetl z trojuhelniku XRP vzdalenost |XP|, co mi vyslo 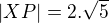 . Ale taky jsem se do toho spis zamotal. Asi by to melo byt jednoduchy, ale nejak mi to proste nevychazi, dik za pomoc.
. Ale taky jsem se do toho spis zamotal. Asi by to melo byt jednoduchy, ale nejak mi to proste nevychazi, dik za pomoc.
Offline
- (téma jako vyřešené označil(a) JohnPeca18)
#2 23. 05. 2013 15:58 Příspěvek uživatele MirekH byl skryt uživatelem MirekH. Důvod: chybně jsem počítal
#4 23. 05. 2013 16:13
Re: Analyticka geometrie
Ahoj, jestliže jsi došel k 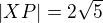 , tak pak víš, že
, tak pak víš, že  leží na průniku kružnice s poloměrem
leží na průniku kružnice s poloměrem  a středem
a středem  a kružnice s poloměrem
a kružnice s poloměrem  a středem
a středem  . Rovnice jsou celkem jednoduché, výsledek jsem ověřil, vychází to.
. Rovnice jsou celkem jednoduché, výsledek jsem ověřil, vychází to.
Pro kontrolu: Souřadnice  jsou
jsou ![kopírovat do textarea $[2;7]$](/mathtex/8f/8fd279e071944991afb06f876699059c.gif) a
a ![kopírovat do textarea $[2;3]$](/mathtex/47/47b703b4e59372073e0d5c7c207bdefa.gif) .
.
ŘEŠTE FYKOS!
Offline
#5 24. 05. 2013 09:04
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Analyticka geometrie
Dekuji, za odpovedi, resil jsem to jak psal ↑ Rumburak:. Nejdriv me matlo, ze tam mam 3 neznami, ale kdyz tam pridam podminku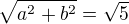
Tak to vychazi.
Offline
![kopírovat do textarea $M[m, n]$](/mathtex/7e/7e841909391cffa5e96d68e279249200.gif) od přímky
od přímky  o rovnici
o rovnici  je rovna
je rovna 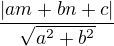 .
. 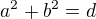 , kde
, kde  je jinak libovolné číslo.
je jinak libovolné číslo.  .
.