Matematické Fórum

smajdalf · 29. 05. 2013 16:43

Zdravím všechny, potřeboval bych pomoct s jedním důkazem:

Dokažte, že zlomek $\frac{7^n + 1}{3^n + 1}$ , kde n je liché přirozené číslo, lze vždy krátit číslem 4.

Já jsem na to šel takto:
$\frac{7^n + 1}{3^n + 1} = \frac{(8 - 1)^n + 1}{(4 - 1)^n + 1} = \frac{[{n \choose 0} 8^n + {n \choose 0} 8^{n-1} (-1)^1 + \ldots + {n \choose n} (-1)^n] + 1}{[{n \choose 0} 4^n + {n \choose 0} 4^{n-1} (-1)^1 + \ldots + {n \choose n} (-1)^n] + 1}$

a teď tedy celý binomický rozvoj (jak v čitateli, tak ve jmenovateli) je dělitelný 4mi, protože z něho tu 4ku můžu vytknout, až na ten poslední člen + 1:
$\frac {\left[ {n \choose n} (-1)^n \right] + 1}{\left[ {n \choose n} (-1)^n \right] + 1}$

No a pro n liché to bude vždy takto:
$\frac {1 \cdot (-1) + 1}{1 \cdot (-1) + 1} = \frac{0}{0}$

No, ale tady si nejsem jistý, jestli je to správnej finish, protože nulou v 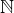$\mathbb{N}$ dělit nelze. Ale zase by to znamenalo, že horní člen $7^n + 1$ je dělitelný 4mi (díky možnosti 4ku z binom. rozvoje vytknout) a ta nula znamená, že beze zbytku. A stejně by to platilo pro jmenovatel.

Je to tak správně, nebo ne?
Poraďte. Díky.

Bati · 29. 05. 2013 17:18

Ahoj,
binomickým rozvojem by to asi šlo taky, ale tady je podle mě pohodlnější použít indukci:

$7^{2k+3}+1=49(7^{2k+1}+1)-48$ , takže jestliže 4 dělí číslo $7^{2k+1}+1$ , tak potom 4 dělí i $7^{2k+3}+1$ . A protože $7^1+1=8$ , platí to pro všechny lichý přirozený k. Stejně se to udělá pro jmenovatel, z čehož plyne, že zlomek se dá krátit 4 pro lichá přirozená k.

vanok · 29. 05. 2013 19:36

Poznamka: staci si vsimnut, ze $7=8-1$ ako aj, ze $3=4-1$ a pouzit binomicky vetu.

smajdalf · 29. 05. 2013 20:36

↑ vanok:
No tu jsem právě použil, ale nejsem si jistej jestli ten závěr $\frac{0}{0}$ , kterej jsem vyvodil, je správně.

P.S.: Nevim jestli si četl můj příspěvek celý, ale je v něm všechno co píšeš. Jak říkám, jen nevím jestli to, že mi vyšlo $\frac{0}{0}$ je z hlediska tohohle důkazu správně (jakože zbytky po dělení čitatele i jmenovatele 4mi jsou 0).

smajdalf · 29. 05. 2013 20:43

↑ Bati:
Tenhle tvůj důkaz vypadá dobře.
Akorát se v tom moc nevyznám (důkazy mi nikdy nešly a asi nikdy nepůjdou).
Mohl bys to prosím tě trochu víc rozepsat.
Matem. indukci znám (samozřejmě), ale v tom tvém důkazu nějak nevidím ten indukční krok.

Díky.

Andrejka3 · 29. 05. 2013 21:09

↑ smajdalf:
$\frac{7^n + 1}{3^n + 1} = \frac{(8 - 1)^n + 1}{(4 - 1)^n + 1} = \frac{[{n \choose 0} 8^n + {n \choose 1} 8^{n-1} (-1)^1 + \ldots + {n \choose n} (-1)^n] + 1}{[{n \choose 0} 4^n + {n \choose 1} 4^{n-1} (-1)^1 + \ldots + {n \choose n} (-1)^n] + 1}$
Pokud je n liche, pak v citateli i jmenovateli posledni clen toho rozvoje je -1. Ta se prictenim jednicky, ktera je uplne na konci vynuluje a zbude v citateli i jmenovateli cislo delitelne 4.
Kdyz jej vytknes , vyjde napriklad v citateli
${n \choose 0} 8^{n-1}\cdot 2 + {n \choose 1} 8^{n-2} (-1)^1\cdot2 + \ldots + {n \choose n-1}(-1)^{n-1}2$ .

smajdalf · 29. 05. 2013 21:24

↑ Andrejka3:
Díky, díky.
Přesně tohle jsem chtěl slyšet.
Takže v podstatě jsem to měl dobře.

Díky všem.

vanok · 29. 05. 2013 23:21

Ahoj ↑ Andrejka3:
Presne toto som nacrtol... A ty si to dokonale rozvinula.

Andrejka3 · 29. 05. 2013 23:36

↑ vanok:
No, on to už autor měl napsané, jen tam udělal chybičku při vytýkání.

vanok · 30. 05. 2013 00:27 — Editoval vanok (30. 05. 2013 00:31)

Vsak aj Neil Armstrong povedal
« That's one small step for [a] man, one giant leap for mankind »
A pre foristov to bol ozaj velky krok.

Matematické Fórum

#1 29. 05. 2013 16:43

Důkaz dělitelnosti

#2 29. 05. 2013 17:18

Re: Důkaz dělitelnosti

#3 29. 05. 2013 19:36

Re: Důkaz dělitelnosti

#4 29. 05. 2013 20:36

Re: Důkaz dělitelnosti

#5 29. 05. 2013 20:43

Re: Důkaz dělitelnosti

#6 29. 05. 2013 21:09

Re: Důkaz dělitelnosti

#7 29. 05. 2013 21:24

Re: Důkaz dělitelnosti

#8 29. 05. 2013 23:21

Re: Důkaz dělitelnosti

#9 29. 05. 2013 23:36

Re: Důkaz dělitelnosti

#10 30. 05. 2013 00:27 — Editoval vanok (30. 05. 2013 00:31)

Re: Důkaz dělitelnosti

Zápatí