Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Průběh funkce - derivace absolutní hodnoty (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 05. 2013 12:02 — Editoval PL4 (31. 05. 2013 12:21)
Průběh funkce - derivace absolutní hodnoty
Zdravím. Mám problémy s derivací absolutní hodnoty, prošla jsem nějaké příspěvky tady a měla jsem dojem, že to chápu, ale pak jsem to zkusila aplikovat na svůj příklad a zas mi to není jasné... Nepřišla jsem na to, jak se v latexu píše značka derivace, tak místo ní používám značku pro stupně.
Chci zderivovat tohle: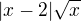
rozepíšu takhle: 
ta absolutní hodnota se (doufám) zderivuje takle:
pak si přepíšu tu absolutní hodnotu tak, aby tam bylo sgn a šlo to vytknout: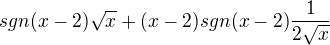
vytknu: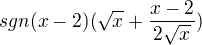
pak: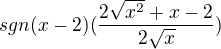
no a teď ten příklad prý pokračuje 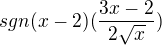
Mám tři otázky:
Chápu tu derivaci té absolutní hodnoty dobře?
Jakto, že se tam ke konci najednou to x na druhou prostě takhle odmocní? Neměla by tam taky být absolutní hodnota?
Ten příklad taky tvrdí, že mi v definičního oboru té funkce vypadly body 0 (jasné) a 2 (?), což mi není jasné. Mám tušení, že by to mohlo být proto, že sgn výrazu nesmí být nula, tak se to vyloučí kvůli tomu, ano?
Moc, moc děkuju komukoli, kdo to dočetl až sem a poskytne mi odpověď na některou z mých otázek.
Offline
- (téma jako vyřešené označil(a) PL4)
#2 31. 05. 2013 12:14
Re: Průběh funkce - derivace absolutní hodnoty
Ahoj ↑ PL4:,
k matematickému problému ako takému sa žiaľ vyjadriť neviem, ale čo sa týka symbolu derivácie, skús zatlačiť Alt a súčasne na numerickej klávesnici vyťukať 39. Malo by to fugovať...
server.gphmi.sk/~domanyov
Offline
#4 31. 05. 2013 12:36 — Editoval Brano (31. 05. 2013 12:36)
Re: Průběh funkce - derivace absolutní hodnoty
↑ PL4:
V akom zmysle potrebujes tu derivaciu, resp. na co ju chces pouzit.
Realna fcia  nie je diferencovatelna v bode
nie je diferencovatelna v bode  ale vsade inde plati
ale vsade inde plati 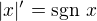
to znamena, ze hoci 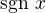 je pre
je pre  definovane -
definovane - 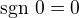 tak ak to je myslene ako ta derivacia, tak
tak ak to je myslene ako ta derivacia, tak  musi vypadnut z def. oboru.
musi vypadnut z def. oboru.
Co sa tyka  tak ano takyto vyraz treba upravit spravne na
tak ano takyto vyraz treba upravit spravne na  avsak uz v zadani bolo
avsak uz v zadani bolo 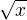 co ma definicny obor
co ma definicny obor  kde mimochodom plati
kde mimochodom plati  .
.
V derivacii este potom vypadnu aj tie body  a nakoniec mas obor
a nakoniec mas obor 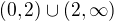 napriek tomu, ze ak by si sa pozrela iba na vyraz
napriek tomu, ze ak by si sa pozrela iba na vyraz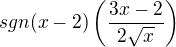
tak ten je definovany na  .
.
Offline
#6 31. 05. 2013 12:52 — Editoval PL4 (31. 05. 2013 13:01)
Re: Průběh funkce - derivace absolutní hodnoty
Potřebuju jí na průběh funkce. To s tím 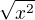 mi vůbec nedošlo, to je jasné, díky.
mi vůbec nedošlo, to je jasné, díky.
Ale to s tou derivací absolutní hodnoty pořád nechápu. Jak bych tedy zderivovala třeba tohle: 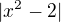 ?
?
Jako: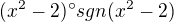 =
= 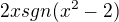
nebo jen: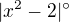 =
= 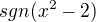
Děkuju.
(Apostrof jsem taky zkoušela.)
Offline
#8 31. 05. 2013 13:38
Re: Průběh funkce - derivace absolutní hodnoty
Mám pocit, že jsem konečně došla k prozření, tak mi to prosím ještě posvěť a budu už naprosto spokojená. Když si tu absolutní hodnotu přepíšu pomocí toho sgn na tvar f(x)sgn(f(x)) a chci to celé zderivovat, tak já si vlastně tu část se signem můžu vyhodit ven, protože je to konstanta a pak tedy zderivuju jen tu část f(x).
Offline
#9 31. 05. 2013 14:14
Re: Průběh funkce - derivace absolutní hodnoty
v podstate ano to co hovoris je toto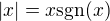 a teda
a teda 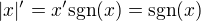
co je v podsate take odvodenie toho vzorca a potom to mozes analogicky pouzit v![kopírovat do textarea $|f(x)|'=[f(x)\text{sgn}(f(x))]'=f'(x)\text{sgn}(f(x))$](/mathtex/67/67324434b146b098d03edccf20f6c13d.gif)
aj ked ja som to myslel skor tak, ze z definicie sa overi a potom na
a potom na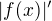 pouzijes vetu o derivovani zlozenej funkcie t.j. najprv derivacia absolutnej hodnoty a potom krat derivacia vnutornej funkcie.
pouzijes vetu o derivovani zlozenej funkcie t.j. najprv derivacia absolutnej hodnoty a potom krat derivacia vnutornej funkcie.
ale ked vysetrujes priebeh tak je mozno jednoduchsie tu absolutnu hodnotu odstranit - t.j. rozdelit definicny obor na  a
a  - tam si tu funkciu upravit tak aby tam ta abs. hodnota nebola a robit dalej s tym
- tam si tu funkciu upravit tak aby tam ta abs. hodnota nebola a robit dalej s tym
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Průběh funkce - derivace absolutní hodnoty (TOTO TÉMA JE VYŘEŠENÉ)