Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 01. 03. 2015 22:20
- cendulka1234

- Příspěvky: 145
- Škola: Mendelova univerzita
- Pozice: student
- Reputace: 2
Re: Parabola a tečna:)
↑↑ misaH:Děkuju moc, už mi to vyšlo :D Jen neumím sčítat a odečítat :D
Offline
#28 01. 03. 2015 22:32
Re: Parabola a tečna:)
Nebo jednodušší počítání:
1) Z rovnice paraboly určíš x-ovou souřadnici bodu T:

![kopírovat do textarea $T[-4;2]$](/mathtex/50/50aae2591bd688b7af13fd0e07f4eaa2.gif)
2) Tečna má obecnou rovnici  . Můžeme předpokládat, že alespoň jeden koeficient je nenulový, zvolíme
. Můžeme předpokládat, že alespoň jeden koeficient je nenulový, zvolíme 
 (vydělíme a)
(vydělíme a)
Označíš:

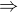


Dosadíš:
Parabola a tečna mají společný bod 


Protože přímka je tečnou, má s parabolou jeden společný bod, proto D=0



3) Dosadíš:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline