Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 06. 2013 12:39 — Editoval found (17. 06. 2013 12:40)
Re: Spojitost fce v A
↑ neznajut:
Ahoj,
doufám, že jsem pochopil správně, že o takové funkci nemůžeme říct, jestli je spojitá nebo ne, i kdybychom si poradili s derivací podle x, jelikož neznáme 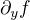 .. Samotný problém vyšetření spojitosti tam, kde je nevlastní derivace (tj. nekonečná) asi není úplně triviální - napadá mě už jen to, že funkce
.. Samotný problém vyšetření spojitosti tam, kde je nevlastní derivace (tj. nekonečná) asi není úplně triviální - napadá mě už jen to, že funkce 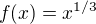 je funkce, která je v bodě
je funkce, která je v bodě 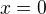 spojitá, ale její derivace jde po stejném vzoru do nekonečna
spojitá, ale její derivace jde po stejném vzoru do nekonečna 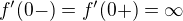 . Jedná se vlastně stejně jako ve tvém příkladě o funkci, která je v daném bodě definovaná, ale její derivace již v tomto bodě definovaná není, pouze na jeho okolí.
. Jedná se vlastně stejně jako ve tvém příkladě o funkci, která je v daném bodě definovaná, ale její derivace již v tomto bodě definovaná není, pouze na jeho okolí.
Asi bych se tedy přiklonil k tomu, že by se hodilo ukázat funkci, o kterou se jedná. :)
J.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#5 17. 06. 2013 23:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost fce v A
↑ neznajut:
Zdravím,
jak může být spojitá, když v bodech s x=0 není definována? Děkuji.
Offline

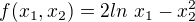
 ?"
?"