Matematické Fórum

Nozyx · 20. 06. 2013 21:03

Počítám příklad

určete souřadnice ohnisek, delky hlavní a vedlejší poloosy a excentricitu elipsy dané rovnicí

$2x^{2}+y^{2}=32$

udělal jsem si abych to dostal do zlomku

$x^{2}+y^{2}/2=32$ ..... ta /2 je jako zlomek

dál udělám $x^{2}/32+y^{2}/64=1$

a ted mam uz rovnici elipsy S[0;0]

a co dal? a mam to dobre vubec? :)

mp3jj · 20. 06. 2013 21:05

↑ Nozyx:
Když rovnici dělíš dvěma, musíš vydělit dvěma i pravou stranu rovnice (tu 32ku) :-)

mp3jj · 20. 06. 2013 21:10

Dále připomenu, že obecná rovnice elipsy je $\frac{(x-m)^{2}}{a^{2}}+\frac{(y-n)^{2}}{b^{2}}=1$

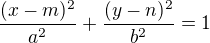
kde $a$ je hlavní poloosa, $b$ vedlejší.
Pro excentricitu platí vzorec $e=\sqrt{a^{2}-b^{2}}$

Teď už to dopočítáš :-)

Nozyx · 20. 06. 2013 21:52

↑ mp3jj: $e=\sqrt{32^{2}-16^{2}}\\ \sqrt{768}$ a to moc umocnit nejde tak c s tim

bonifax · 20. 06. 2013 22:23

↑ Nozyx:

čau, hlavní poloosa ale není 32 ale odmocnina ze 32 a v.poloosa není 16 ale odmocnina ze 16.

tudíž pro e platí: $e=\sqrt{32-16}$ . Koukni se znova na tu rovnici elipsy - $a^2=32$

Matematické Fórum

#1 20. 06. 2013 21:03

elipsa

#2 20. 06. 2013 21:05

Re: elipsa

#3 20. 06. 2013 21:10

Re: elipsa

#4 20. 06. 2013 21:52

Re: elipsa

#5 20. 06. 2013 22:23

Re: elipsa

Zápatí