Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
#1 27. 06. 2013 16:58
Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
Zdravim,
mam ulohu, se kterou si neumim presne rozumove poradit. Myslim, ze by mohla spadat jak do sekce Zakladni skoly, Stredni skoly, tak mozna i Vysoke skoly.
Jedna se celkem o trivialni ulohu. Mam podlahu tvaru ctverce o hrane 5 metru. Pokud rozmistim predmety po mistnosti tak, ze budou tvorit vrcholy ctverce o hrane 1 m, tak budu mit na podlaze celkem 5*5=25 predmetu rovnomerne rozmistenych. Pokud uvazuji uzke predmety (napr. jehly), tak si mohu predstavit, ze zabiraji v pudorysu celkem 25 bodu (jehly jsou zapichnute spickou do podlahy).
Pokud bych vsak chtel podlahu natrit a zjistit obsah podlahy, tj. obsah ctverce o hrane 5 m, tak ziskam obsah 25 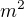 . V obou pripadech dostanu stejne cislo, a to 25.
. V obou pripadech dostanu stejne cislo, a to 25.
Kdyz se nad tim zamyslim, tak v pripade jehel mam po podlaze rozmistenych presne 25 predmetu. Pokud jsou jehly "velmi ostre", tak v limite zabiraji v pudorysu 25 bodu na podlaze. Pokud by byly spicky natrene barvou, mel bych po jejich vytazeni obarveno 25 bodu na podlaze. Pokud ale beru obsah jako natrenou plochu, tak mam vlastne nekonecne mnoho bodu natrenych a pritom je to stejne cislo, ktere bylo spocitano stejnym postupem, tj. 5 krat 5. Kde je problem?
Vim, ze to nejak mozna souvisi s teorii miry, ale to je dost pokrocila oblast matematiky, do ktere moc nevidim..Muze mi tohle nekdo prosim vysvetlit? Diky
Offline
#2 27. 06. 2013 17:40
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Andrew123:
Ahoj.
Nevím, zda rozumím, co přesně máš na mysli. Ale zmiňuješ-li se o teorii míry, tedy:
Míra je - shruba řečeno - funkce, která každé množině z určitého systému přiřadí nějakou nezápornou číselnou hodnotu (může být i nekonečná).
Abychom mohli opravdu hovořit o míře, musí ten množinový systém mít určité vlastnosti a musí i ta funkce mít určité vlastnosti.
Mírou je např. funkce, které dané množině přiřazuje počet jejích prvků. To je tzv. diskretní míra.
V eukleidovských prostorech dimensí 1, 2, 3 máme dále eukleidovské míry (délka, plošný obsah, objem) .
Takže za problém považuješ fakt, že plošná míra jedné množiny (podlahy) vyšla stejně jako diskretní míra jiné množiny (množiny jehel)?
Offline
#3 29. 06. 2013 22:14
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Rumburak:
Ahoj,
diky za reakci, prakticky ano, i kdyz citim ten rozdil u diskretni mnoziny a podlahy. No mozna jsem to zbytecne zeslozitil. Jde mne spise o to, jak vysvetlit, proc obsah ctverce se rovna prave 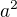 . Intuitivne je to celkem jasne, pocita se s tim uz zakladni skoly a nikdo se nad tim nepozastavuje.., ale proc je vztah prave takovyto? Jake je vysvetleni, ze se obsah ctverce pocita prave takto? Vysvetleni jsem nikde nenasel.
. Intuitivne je to celkem jasne, pocita se s tim uz zakladni skoly a nikdo se nad tim nepozastavuje.., ale proc je vztah prave takovyto? Jake je vysvetleni, ze se obsah ctverce pocita prave takto? Vysvetleni jsem nikde nenasel.
Offline
#4 30. 06. 2013 18:11 — Editoval martisek (30. 06. 2013 18:12)
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Andrew123:
Ahoj,
vysvětlení ani nikde nenajdeš. Je to totiž axiom. Stejně jako nevysvětlíš, proč dvěma různými body prochází právě jedna přímka, anebo proč pravděpodobnost jistého jevu je jedna. Není to nic jiného než matematický popis věcí, které tak prostě fungují.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#5 01. 07. 2013 09:47 — Editoval Rumburak (01. 07. 2013 09:56)
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Andrew123:
Nebo si polož otázku: Na kolik čtverečků o straně délky 1 (předpokládám, že délková jednotka je již stanovena) lze rozdělit
čtverec o straně délky
(1)  ?
?
Snadno si spočítáš, že těch čtverečků bude  . Takže prohlásíme-li plošný obsah čverce o jednotkové délce strany
. Takže prohlásíme-li plošný obsah čverce o jednotkové délce strany
za jednotku plošného obsahu, potom výše uvažovaný čtverec o straně délky  splňující (1) bude mít obsah
splňující (1) bude mít obsah  .
.
Tuto zkušenost zobecníme i na čtverec, u něhož délka strany  není nutně přirozené číslo: jeho obsah DEFINUJEME
není nutně přirozené číslo: jeho obsah DEFINUJEME
hodnotou 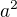 , což s úvodní zkušeností není v rozporu.
, což s úvodní zkušeností není v rozporu.
Dalším zobecněním by byl vzorec definující obsah obdélníka.
Offline
#6 08. 07. 2013 11:34 — Editoval Rumburak (11. 07. 2013 09:26)
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Andrew123:
Dodatečně mne napadl způsob, jak od praktických hledisek dojít ke vzorci pro obsah obdélníka.
Především chceme zajistit, aby shodné obdélníky měly shodné obsahy. To znamená, že obsah obdélníka musí být
vyjádřitelný jako funkce pouze jeho rozměrů (tj. délek sousedních stran měřených v týchž jednotkách).
Předpokládejme tedy, že  , a označme
, a označme 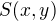 obsah odélníka o rozměrech
obsah odélníka o rozměrech  .
.
Na funkci  budeme klást další požadavky, které prohlásíme za axiomy:
budeme klást další požadavky, které prohlásíme za axiomy:
(1)  ,
,
(2) 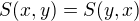 ,
,
(3) je-li též  , potom
, potom  .
.
K axiomům (1), (2) jistě netřeba komentáře. Axiom (3) popisuje situaci, kdy dva sousedící obdélníky o rozměrech  resp.
resp.  společně vyplňují obdélník o rozměrech
společně vyplňují obdélník o rozměrech  .
.
Další postup bude již ryze deduktivní. Ve všech následujících úvahách stále předpokládáme  .
.
Označme ještě  .
.
Lemma 1. Je-li  , potom
, potom  .
.
Důkaz.
Lemma 2. Je-li
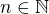 , potom
, potom 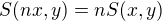 .
. Důkaz snadno provedeme úplnou indukcí.
Lemma 3. Je-li
 racionální číslo, potom
racionální číslo, potom 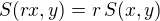 .
. Důkaz.
Lemma 4. Je-li
 , potom
, potom 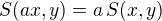 .
. Zbývá dokázat případ, kdy
 není rac. číslo.
není rac. číslo. Nyní již snadno dojdme k cílovému tvrzení:
Věta. Je-li
 , potom
, potom 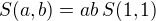 .
. Důkaz.
Číslo
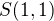 zřejmě představuje obsah čtverce o straně délky 1, kterýžto obsah zpravidla považujeme za jednotkový,
zřejmě představuje obsah čtverce o straně délky 1, kterýžto obsah zpravidla považujeme za jednotkový, takže klademe
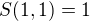 .
.Měli bychom též zpětně ověřit, že funkce
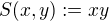 definovaná pro
definovaná pro  vskutku vyhovuje
vskutku vyhovuje axiomům (1), (2), (3), což není nijak obtížné.
Offline
#7 10. 07. 2013 12:33
Re: Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry
↑ Rumburak:
OK, děkuji moc za ochotu a vysvětlení. Zkusím to nějak "vstřebat".
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Presne pochopeni slova "obsah utvaru" X "pocet bodu"; Teorie miry

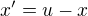 , tj.
, tj. 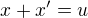 . Z předpokladu
. Z předpokladu  , odtud a dle (3) pak
, odtud a dle (3) pak  , neboli
, neboli 
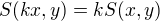 .
.  taková, že
taková, že 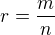 .
. 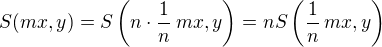 ,
, 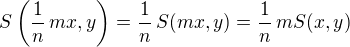 ,
,  kladných racionálních čísel takové, že
kladných racionálních čísel takové, že  ,
, 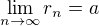 ,
,  ,
, 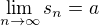 .
.  ,
, 
 (dle lemmatu 1) ,
(dle lemmatu 1) ,  (dle lemmatu 3) .
(dle lemmatu 3) .  ,
,  , odtud
, odtud 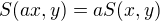 .
.  .
.