Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 07. 2013 13:45
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Zmena akcelerácie za čas - vzorce
Zdravím. Chcel som si sám vyvodiť vzorce pre "ryv"(j) (neviem, či je to správny názov pre tretiu deriváciu polohy podľa času). A postupoval som nasledovne:
j = a / t
j = v / t / t
j = v / t^2
v = j * t^2![kopírovat do textarea $s = \int_{0}^{t} j * t^2 = j * \int_{0}^{t} t^2 = j * [ \frac{1}{3}t^3 - \frac{1}{3}0^3 ] = \frac{1}{3}jt^3$](/mathtex/51/510c958fbada6d76d0d6da55b6179b66.gif)
ale keď som tieto vzorce hľadal na internete našlo mi  Tak kde mám chybu ? Vopred ďakujem.
Tak kde mám chybu ? Vopred ďakujem.
Offline
- (téma jako vyřešené označil(a) GeekRobert)
#2 02. 07. 2013 13:48
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Re: Zmena akcelerácie za čas - vzorce
Vyšlo by mi to ak by som ako vzorec pre rýchlosť použil 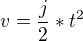
ale pri spätnej úprave by som dostal 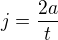
Čo je podľa mna nezmysel ...
Offline
#3 02. 07. 2013 14:17
Re: Zmena akcelerácie za čas - vzorce
↑ GeekRobert:
Tedy, poprvé slyším o nějakém "ryv", ovšem pokud je to třetí derivace podle času, pak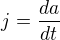 , a ne
, a ne 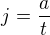 , tam bude počátek Vašich problémů.
, tam bude počátek Vašich problémů.
Je-li 'j' konstanta, pak postupnou integrací
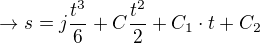
Pokud budou integrační konstanty podle počátečních podmínek nulové, dostáváte 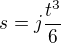
Pokud se tedy nemýlím.
Offline
#4 02. 07. 2013 14:28
Re: Zmena akcelerácie za čas - vzorce
↑ GeekRobert:
Ty totiž montuješ dohromady dvě různé "věci" - obecné vztahy mezi kinematickými veličinami (integrály) a rovnoměrně zrychlený pohyb ( ), kde je zrychlení konstanta, což zde obecně není.
), kde je zrychlení konstanta, což zde obecně není.
Takže mějme 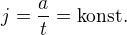 , pak
, pak 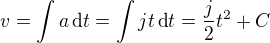 a to vůbec není nesmysl (příspěvek #2)
a to vůbec není nesmysl (příspěvek #2)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 02. 07. 2013 16:28
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Re: Zmena akcelerácie za čas - vzorce
A aký je pre to názov ? V angličtine sa to volá Jerk a na wikipedii na stránke "Derivácia" bolo napísané "Ryv - Tretia derivácia polohy podľa času".
A díky za odpovede.
Offline
#6 02. 07. 2013 16:31
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Re: Zmena akcelerácie za čas - vzorce
A ake vzorce by pripadne boli pre štvrtu derivaciu polohy ??
Offline
#7 02. 07. 2013 16:38
Re: Zmena akcelerácie za čas - vzorce
↑ GeekRobert:
Jak jsem googloval, tak název i význam je takový, jaký uvádíte. To, že já jsem to dnes viděl poprvé, nic neznamená. Zřejmě jde o běžný pojem.
Pokud se tedy nemýlím.
Offline
#8 02. 07. 2013 23:52
Re: Zmena akcelerácie za čas - vzorce
Ahoj,
třetí derivace se vážně označuje jako ryv, to jsem si kdysi hledal na začátku studia na vejšce.
Jak psal Zdeněk, problém je u tebe v obecných vztazích. Obecně totiž vše vypadá takto:
Čtvrtá derivace bude vypadat takto
Pátá zase takto
Můžeš takhle pokračovat do nekonečna, jenže to už je tak nějak zbytečné. Teď je tvojí otázkou zřejmě to, jak se bude chovat změna polohy - nějaká dráha, tedy  , pro jednoduchost a názornost to ukážu pro jednodimenzionální pohyb, kdy
, pro jednoduchost a názornost to ukážu pro jednodimenzionální pohyb, kdy  a tedy
a tedy 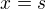 .
.
Obecně zase bychom řešili spoustu integrálů. Ty se totiž vždycky ptáš na speciální případy...
1) když je ryv nulový, co se děje?
2) když je ryv konstantní, co se děje?
3) když je ryv lineární, co se děje?
4) když je ryv kvadratický, co se děje?
...
Většinou se v téhle úvodní části ptáme jenom na tyhle "polynomální" závislosti, ovšem třeba v případě pružiny už je situace komplikovanější. Takže zkusíme vyřešit alespoň tyhle
Pro závislost
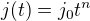 tedy vychází
tedy vychází
Poslední vztah lze ještě přepsat (dle mého hezčím způsobem) na

Tak doufám, že jsem uspokojil tvou zvědavost po "obecnosti" :)
S pozdravem
J.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#9 03. 07. 2013 09:39
- GeekRobert

- Příspěvky: 65
- Škola: SPŠ J.Murgaša
- Pozice: Študent
- Reputace: 0
Re: Zmena akcelerácie za čas - vzorce
Ďakujem všetkým za vysvetlenie a objasnenie.
Offline

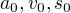 jsou jasné, co znamenají.
jsou jasné, co znamenají.

