Matematické Fórum

cmaxi · 14. 07. 2013 20:12 — Editoval jelena (15. 07. 2013 23:05)

Jelena: přesun do AaP, prosím, kolega studuje ZŠ. Děkuji.

Zdravím, jak co nejefektivněji vypočítat zbytek velké mocniny? Např. 12374870^7494583 mod 13123753.

Mám v plánu to dát do programu, který by to počítal, avšak přesahuje to maximální počet číslic. :) upřesněno

Děkuji

Miky4 · 14. 07. 2013 22:22

↑ cmaxi:
Zdravím, potřebuješ to jen na tento konkrétní příklad?

cmaxi · 14. 07. 2013 22:35

Potřebuju to na různé čísla, potřeboval bych postup.

cmaxi · 15. 07. 2013 09:37

Nejspíš bych k tomu měl použít čínskou větu o zbytcích, ale vůbec ji nechápu.

Cheop · 15. 07. 2013 09:45

↑ cmaxi:
A podle tohoto to nenaprogramuješ?
čínská věta

cmaxi · 15. 07. 2013 09:51

Já jsem to na wiki našel, ale to moc nechápu jak mám postupovat, rozložit na prvočísla zvládnu, Eulerovu funkci asi taky, ale ten zbytek s M1 a dál už ne.

jelena · 15. 07. 2013 10:29

↑ cmaxi:

Zdravím,

Tvé téma přesunu do sekce "Algoritmů a programování". Na výpočet zbytků jsou "standardní kódy", ale určitě bude pro kolegy snadnější, pokud upřesníš: co programuješ, v čem programuješ, případně Tvé kódy (část, která je problémová), zda potřebuješ něco mít více efektivní apod.

V jiném tématu jsi uvedl, že studuješ ZŠ, ale teď je to různé - jeden studuje ZŠ a má samostudiem široký rozhled a teoretické/praktické znalosti, jiný studuje VŠ a nemá nic, ani znalosti MŠ. Tedy dej, prosím, odkazy, co jsi prostudoval a co je ještě srozumitelné a kde je třeba vysvětlovat.

Řekla bych, že dobré materiály jsou zde, ale tento materiál, na který se odkazuje z KSP je třeba pro mne moc těžký. Tak to ještě upřesní, prosím. Ať se za pomocí kolegů podaří. Kolegům děkuji.

cmaxi · 15. 07. 2013 11:02

V podstatě potřebuji poznat RSA šifrování, které se ukázalo jako trochu komplikovanější než jsem myslel.

Šifrování probíhá tak, že mám nějaký číslice např. 52 a exponent např. 1253.
Šifrování = 52^1253 mod 3222

Dešifrování vypadá obdobě:
Dešifrování = Šifrování^52853 mod 3222

Tyto čísla jsou vymyšlené, takže by to asi nevyšlo. :)

Programuji ve visual basicu a v C#, tento projekt však mám rozdělaný v basicu.
A pokud se nemýlím, tak maximální velikost je 128 nebo 96 bit, což je pro větší konečná.

Potřebuji tedy vypočítat zbytek bez toho, abych počítal mocninu. Na wikipedii tohle přesně je.

Mě by stačilo, aby někdo tady mi napsal jak se postupovalo a já to snad už dál zvládnu.

kexixex · 16. 07. 2013 14:25

↑ cmaxi:
Ahoj,
myslim, ze se zakladnimi datovymi typy si u RSA nevystacis. Budes muset reprezentovat cislo jako retezec znaku a naprogramovat si aritmetiku (viz napriklad zde).

mák · 16. 07. 2013 15:33

Zdravím,

Cheop napsal(a):
čínská věta

Tohle je fakt jednoduchý a hlavně rychlý, mnohem rychlejší než zabudované mod a hlavně to umí velký čísla. Nepotřebuješ žádné velké datové typy.
Zkusil jsem to v mé oblíbené maximě, zde je celý kód (za správnost neručím, ale co jsem zkusil několik čísel, tak vypadá, že funguje):

Code:

Zbytek(Num, Exp, Z):=block([s,z,Fi,Le,Ef,Ms,Zs,Mi,Ni,Ki],
    s: ifactors(Z),
    Fi: maplist(lambda([z],z[1]^z[2]),s),
    Le: length(Fi),
    Ef: maplist(lambda([z],EulerFu(z)),Fi),
    Ms: mod(Exp,Ef),
    Zs: makelist(mod(Num^Ms[i],Fi[i]),i,1,Le),
    Mi: makelist(Z/Fi[i],i,1,Le),
    Ni: makelist(mod(Mi[i],Fi[i]),i,1,Le),
    Ki: makelist(inv_mod(Mi[i],Fi[i]),i,1,Le),
    mod(apply("+",Zs*Mi*Ki),Z)
);

Konverze do Visual Basicu by asi šla. Nejhorší je příkaz ifactors - rozloží číslo na prvočísla.
maplist se dá nahradit smyčkou for in
makelist se dá nahradit smyčkou for next
mod je identický ve VB
inv_mod je inverzní modulo a asi se bude muset naprogramovat
EulerFu je Eulerova funkce - jednoduše se dá naprogramovat - v maximě:

Code:

EulerFu(n):=block([z],
    apply("*",flatten(maplist(lambda([z],z[1]^z[2]*(1-1/z[1])),ifactors(n))))
);

cmaxi · 17. 07. 2013 17:30

S prvočísli není žádný problém, na to jsem už program udělal.

cmaxi · 17. 07. 2013 18:15 — Editoval cmaxi (17. 07. 2013 18:16)

Mohli byste mi prosím napsat, jak by se řešil tento príklad?:
$123 ^ {17}$ mod 3233
3233 = 53*61

mák · 17. 07. 2013 20:35

Zkusím krok za krokem - použiji výše uvedený postup z Wikipedie.

Základ = 123
Exponent = 17
Dělitel = 3233

Dělitel si rozložím na prvočísla = 53 * 61
P1 = 53
P2 = 61

Následují výpočty - vždy první řádek patří k prvnímu prvočíslu a druhý k druhému.
Pokud se dělitel rozloží na 5 prvočísel, bude ke každé operaci příslušet 5 řádků.

Vypočtu si ke každému z nich Eulerovu funkci:
F1 = phi(P1) = phi(53) = 52
F2 = phi(P2) = phi(61) = 60

Tyto hodnoty použiji ke zmenšení exponentu (v tomto případě je exponent velmi malý tak není vidět výsledek):
Q1 = mod(Exponent, F1) = mod(17, 52) = 17
Q2 = mod(Exponent, F2) = mod(17, 60) = 17
To jsou dva rozdílné výsledky i když vypadají stejně, ale jeden přísluší k prvnímu prvočíslu a druhý k druhému.

Teď přijde operace při které jsem si uvědomil, že si s běžnými datovými typy nevystačíme. Byl jsem zaslepen zkouškami s dvoumístným základem a tam mi to vycházely i s velmi velkými exponenty malá čísla.

Umocníme základ ne exponentem, ale číslem které vyšlo při minulé operaci. (Tím se zmenší číslo s kterým budeme pracovat. V tomto případě ale ne.) A provedeme modulo s každým prvočíslem.
Q1 = mod(Základ^Q1, P1) = mod(123^17, 53) = 7
Q1 = mod(Základ^Q2, P2) = mod(123^17, 61) = 1

Vypočítáme si "doplněk" ke každému prvočíslu:
M1 = Dělitel/P1 = 3233/53 = 61
M2 = Dělitel/P2 = 3233/61 = 53
Zde je to to druhé prvočíslo, ale pokud bude více prvočísel, vyjde součin zbývajících prvočísel.

Vypočítáme inverzní modulo:
N1 = inv_mod(M1, P1) = inv_mod(61, 53) = 20
N2 = inv_mod(M2, P2) = inv_mod(53, 61) = 38

Teď už bude společná operace pro všechny výsledky posledních třech výpočtů:
(Q1*M1*N1) + (Q2*M2*N2) = (7 * 61 * 20) + (1 * 53 * 38) = 10554
A toto zredukované číslo použijeme pro závěrečný výpočet:
Zbytek = mod(10554, 3233) = 855
Což je výsledek.

cmaxi · 17. 07. 2013 21:49 — Editoval cmaxi (18. 07. 2013 00:10)

Jsem naschával zvolil 17, protože to nelze zmenšit, tak nevím co s tím, 123^17 s mod 3233 možná šel rozdělit:
1x123 mod 3233 = 123 (1x)
123x123 mod 3233 = 2197 (2x)
2197x123 mod 3233 = 1892 (3x)
1892x123 mod 3233 = 3173 (4x)
3173x123 mod 3233 = 2319 (5x)
2319x123 mod 3233 = 733 (6x)
733x123 mod 3233 = 2868 (7x)
2868x123 mod 3233 = 367 (8x)
367x123 mod 3233 = 3112 (9x)
3112x123 mod 3233 = 1282 (10x)
1282x123 mod 3233 = 2502 (11x)
2502x123 mod 3233 = 611 (12x)
611*123 mod 3233 = 794 (13x)
794x123 mod 3233 = 672 (14x)
672x123 mod 3233 = 1831 (15x)
1831x123 mod 3233 = 2136 (16x)
2136x123 mod 3233 = 855 (17x)

Ale asi by to bylo zdlouhavé. :(

Anebo:
To nechat a zkrátit co to jde a pak to jednoduše vypočítat, koukal jsem, že v Framework 4.5 je nyní BigInteger, který není nijak omezený. :) Ale nevím, zda je to praktické.

EDIT: A ještě moc nechápu inverzní modulo, na wiki o čínské větě:

M1 = 13 · 17 = 221
$N_1 = M_1^{–1} = 100^{–1} = 23 Z_{121}$

Proč 1/100 = 23 (mod 121)?
A proč $221^{–1} = 100^{–1}$

kexixex · 18. 07. 2013 13:05

↑ cmaxi:
K inverznim prvkum.. Reknem ze a je inverzni k b, pokud a"krat"b=1. Piseme $a=b^{-1}$ . Jenze co je to "krat"? Pokud pocitas "modulo neco", neni to "krat" stejne krat jako v celych cislech. Operace "krat" v $\mathbb{Z}_{121}$ vlastne rika: (1) Vynasob operandy jako v celych cislech. (2) vrat zbytek po deleni cislem 121., pricemz krok (1) je jenom pomucka, jak se dobrat k vysledku.

Takze plati 100"krat"23=1 (mod 121), takze 100 je inverzni prvek k 23 v $\mathbb{Z}_{121}$ vzhledem k operaci "krat".

Jestli to chces opravdu chapat, asi ti nezbyde nez zacit s nejakou ucebnici algebry nebo teorie cisel pekne od zacatku, nebo si detailne prostudovat a pochopit napr. material od jeleny vyse.

Jinak co se mocneni tyce, tvuj postup (posutpne nasobit a modulit) by samozrejme fungoval, jen by byl opravdu zdlouhavy, rychlejsi algroitmus je popsan tady. Naopak na hledani inverzu se da pouzit algoritmus zde.

Honzc · 18. 07. 2013 14:03 — Editoval Honzc (18. 07. 2013 14:05)

↑ cmaxi:
Píšeš:
Proč 1/100 = 23 (mod 121)?
A proč $221^{–1} = 100^{–1}$
1.To $(100)^{-1}$ neznamená $\frac{1}{100}$ , to je jen nějaká definice.
2. $M_{1}=221\; mod \;121\equiv 100$
Pak podle definice máme: $N_{1}=(100)^{-1}$
Jak z toho teď spočítat jaký bude zbytek po dělení číslem 121?
Musí platit tato rovnice (v přirozených číslech)
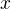$x\cdot 100=y\cdot 121+1$ kde to $x$ bude ten náš hledaný zbytek
Pak zbývá v celých číslech vyřešit $x =\frac{y\cdot 121+1}{100}$
To není těžké vyřešit zkusmo uvědomíme-li si, že
$y\cdot 121$ musí končit číslicemi 99 (aby, když přičteme 1) byly na konci 2 nuly.
Tedy stačí vyzkoušet postupně čísla $y=9,19,29,...119$
Hned při $y=19$ dostaneme $19\cdot 121+1=2299+1=2300$
a pak $x=\frac{2300}{100}=23$ což je i zbytek po dělení číslem 121.
Obdobně si to můžeš vyzkoušet pro $M_{2}->N_{2}$
$2057=158\cdot 13+3\equiv 3 (mod\;13)$
pak $x=\frac{y\cdot 13+1}{3}$
a tedy $x=\frac{2\cdot 13+1}{3}=9$