Matematické Fórum

bejf · 20. 07. 2013 13:50

Ahoj, potřeboval bych poradit s jedním zřejmě lehkým příkladem.

Napište parametrické rovnice přímky procházející bodem C a rovnoběžné s přímkou AB.
Přičemž víme, že $A[1;1], B[1;3], C[0;3]$ .

Já jsem nejdřív zjistil směrový vektor přímky AB.
$B-A=(0;2)$
Aby byla druhá přímka rovnoběžná, potom bude mít stejný směrový vektor jako AB nebo k-násobek tohoto směrového vektoru.
Já jsem použil 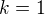$k=1$ , tedy stejný směrový vektor.

Pak mi vychází parametrické vyjádření
$x=0+0t\nl y=3+2t$
resp.
$x=0\nl y=3+2t$

Postup by snad měl být správně.
Jenže ve výsledcích je uvedeno, že má být
$x=0\nl y=t$

Když si to nakreslím, tak by to odpovídalo, ale nedaří se mi k tomu dojít početně. Díky za odpovědi.

Hanis · 20. 07. 2013 14:11

Ahoj,

oba výsledky jsou správně, když označíš 3+2t=u, tak dostaneš ten stejný popis... využiješ toho, že x-ová souřadnice není závislá na parametru a jak 3+2t tak i u probíhá všechna reálná čísla.

bejf · 20. 07. 2013 14:27

↑ Hanis:
Jasně, takže prostě když bych potom hledal jakýkoli bod z této přímky rovnoběžné k AB (podle zadání), tak ten bod bude mít vždy souřadnice $[0;y], y\in R$ .

Hanis · 20. 07. 2013 14:44

Ano.

Matematické Fórum

#1 20. 07. 2013 13:50

Analytická geometrie - vzájemná poloha přímek

#2 20. 07. 2013 14:11

Re: Analytická geometrie - vzájemná poloha přímek

#3 20. 07. 2013 14:27

Re: Analytická geometrie - vzájemná poloha přímek

#4 20. 07. 2013 14:44

Re: Analytická geometrie - vzájemná poloha přímek

Zápatí