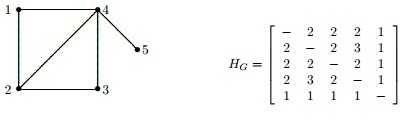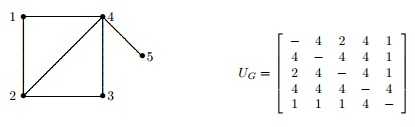Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 07. 2013 02:59
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
Začal bych tím, co je vlastně hranová/uzlová souvislost? Respektive hranový/uzlový řez.
Hranový řez (mezi dvěma uzly třeba  a
a  ) je množina hran
) je množina hran  taková, že každá cesta z
taková, že každá cesta z  do
do  má alespoň jednu hranu v
má alespoň jednu hranu v  . A navíc, žádná vlastní podmnožina tuto vlastnost nesplňuje.
. A navíc, žádná vlastní podmnožina tuto vlastnost nesplňuje.
Zjednodušeně lidsky řečeno, je to množina hran, které musíš odstranit, aby se graf rozpadl a zároveň uzly x a y byly v různých komponentách. Navíc s touhle vlastností minimální.
V matici je na pozici i,j nejmenší počet těch hran, které musíš odstranit, aby se graf rozpadl a i a j byly v jiných komponentách (tzv. hranový stupeň souvislosti mezi dvěma uzly).
Takže v tom tvém případě, mezi uzly 4 a 5 je to jednoduché -> odstraníš jednu hranu a máš rozpadnuto.
Když bys chtěl "odříznout" 2 od 4, musíš uříznout 3 hrany.
atd...
Uzlová souvislost je analogií. Jen je "problém" v případě sousedních prvků. V případě, že jsou uzly sousední je uzlový stupeň roven 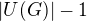
Offline
#3 24. 07. 2013 12:17
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Tu hranovou souvislost jsem nějak tak, jak popisuješ chápal, ale nevěděl jsem co s to uzlovou souvislostí. Např. u hrany 1,2 v uzlové matici souvislosti jsem nechápal, proč je tam ta 4. Podle Tvé poslední věty mám tedy chápat, že vzhledem k tomu, že 1,2 jsou sousedními prvky a U(G) = 5 (počet řádků matice), tak výsledek bude 5 - 1 = 4?
Např u prvku 1,3 je mi jasné, že musím odstranit uzel 2 a 4, aby vzniknul řez - tudíž výsledek rovná se 2.
Offline
#4 24. 07. 2013 12:56
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Chápeš to správně.
Pokud máš dva uzly, které jsou sousední tak nikdy nemůžeš odstraněním nějakých uzlů dosáhnout toho aby byly v různých komponentách - kvůli té hraně která je spojuje. Proto se definuje tenhle případ "speciálně".
A ještě slovíčkaření na konec: 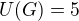 a
a  jsou dvě rozdílný věci. Vzhledem k tomu, že moje vyjádření bylo taky trochu vágní je to samozřejmě jedno, ale jestli je váš profesor puntíčkář, jak jsem četl v nějakém Tvém příspěvku, tak jenom doplňuji.
jsou dvě rozdílný věci. Vzhledem k tomu, že moje vyjádření bylo taky trochu vágní je to samozřejmě jedno, ale jestli je váš profesor puntíčkář, jak jsem četl v nějakém Tvém příspěvku, tak jenom doplňuji.
Offline
#5 24. 07. 2013 13:24
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Ok, děkuji. Navázal bych na další věc, kterou v tomto tématu nechápu a sice tento vztah: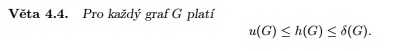
zdroj: http://favwiki.jenda.eu/ftp/kma/tgd1/tgd1_pracovni.pdf (27. strana)
Pokud bych měl tento graf: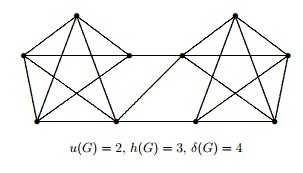
Jak zjistím u(g) a h(g)? Vytvořil bych si opět matice, jako výše a vybral nejmenší prvek? Minimálním stupněm grafu se rozumí co (definici znám, jde opět spíš o to lidské vysvětlení :-))?
Offline
#6 24. 07. 2013 14:05 — Editoval ondrej.hav (27. 07. 2013 17:18)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Stupeň uzlu je počet hran, které ten uzel obsahuje. Minimální stupeň grafu je potom nejmenší ze všech stupňů uzlů. V tomhle případě mají všechny uzly stupeň 4 nebo 5 (snad jsem se nepřekoukl). Tudíž minimální stupeň grafu je 4.
co se týče hranového/uzlového stupně souvislosti grafu tak jak říkáš, můžeš si vytvořit matice a vybrat nejmenší prvky.
Nicméně, celá matice je zbytečně "velká věc". Lidsky řečeno, musíš najít nejmenší řez (hranový/uzlový) který ti rozdělí ten graf na komponenty. Nepotřebuješ to zjišťovat mezi všemi dvojicemi. Ty grafy většinou bývají konstruovány tak, aby to bylo snadné.
V tomhle případě když bys to "rozřízl" uprostřed (odstranil ty hrany, které tvoří jakési Z) tak dostaneš dvě komponenty. Takže si uděláš takovýhle "odhad" a pak už se jenom zamyslíš, jestli to může být i menší? Tedy jestli by ti stačilo odstranit 2 hrany aby se ten graf rozpadl. Jelikož ty dvě "půlky" grafu jsou "skoro" úplné grafy, tak nejspíš ne.
Uzlový řez je podobný. Zvolíš si uzlový řez velikosti 2, ten snad vidíš. A zeptáš se sám sebe "je možné mít menší řez?" tedy řez velikosti 1? No, evidentně ne.
Pokud to v tom grafu nevidíš, můžeš udělat i matice, ale v tomhle případě je to matice o 10x10 a to není málo. Ikdyž jsou ty matice symetrické a diagonálu neřešíš i tak ti zbývá 45 prvků. Takže ani polynom nemusí být pro člověka dostatečně rychlý.
Mimochodem, daleko "zajímavější" je ten druhý graf z těch skript.
Offline
#7 24. 07. 2013 15:59
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Aha, aha, myslím že věta "musíš najít nejmenší řez (hranový/uzlový) který ti rozdělí ten graf na komponenty" mi to všechno objasnila. Zkoušel jsem i ten druhý graf ze skript a to řešení mi vyšlo stejně.
Mohl bys mi prosím objasnit ještě poslední věc a sice tyto dvě věty: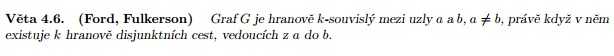
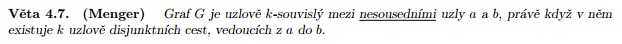
Co to je hranově disjunktní cesta? K čemu mi tyto věty vlastně jsou?
Offline
#8 24. 07. 2013 17:25 — Editoval ondrej.hav (24. 07. 2013 17:33)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Hranově disjunktní cesty jsou takové, které prostě nevedou přes stejné hrany. Představ si graf na obrázku...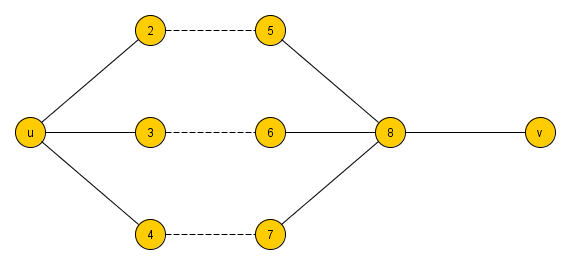
mezi u a v existuje několik cest, jak vidíš (např.: u,2,...5,8,v). Ale nejsou hranově disjunktní, protože nakonec vždycky použiješ hranu (8,v). Tudíž je zde jenom jedna hranově disjunktní cesta. A je zde krásně vidět, že mezi uzly u a v je graf 1 souvislý, protože stačí odebrat jednu hranu a stane se nesouvislým.
Význam těchto vět je především v jejich důkazu. Důkazy obou vět totiž ukazují algoritmy, jakým převést problém k-souvislosti na problém toků. V tom je velká síla především v otázce příslušnosti k třídám složitosti. Z toho všeho nakonec totiž plyne, že k-souvislost náleží P. Díky převodu na toky, které jsou polynomiální. Na to se Ryjáček ptá ;)
EDIT: Teď na to tak koukám, nevysvětlil jsem to úplně ideálně. Takže doplním trošku lepší definici těch disjunktních cest: Dvě cesty p1 a p2 jsou hranově disjunktní, pokud žádná hrana není ZÁROVEŇ v p1 i p2. Takhle se mě to líbí víc ;) Ale pořád je to snad user-friendly.
Offline
#9 24. 07. 2013 18:04 — Editoval Shelber (24. 07. 2013 18:09)
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Takže mohu říct, že graf na obrázku je hranově 1-souvislý mezi uzly u a v (dle FF)?
Offline
#10 24. 07. 2013 18:08
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Ano.
Offline
#11 24. 07. 2013 18:09
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Děkuju.
Napsal bys mi prosím ještě nějaké rady, na co se zaměřit při učení? Zkoušku mám, jak si správně uhádl u Ryjáčka (předmět teorie grafů a disk. optimalizace). Pochopil jsem, že už máš zk. za sebou?
Offline
#12 24. 07. 2013 18:11 — Editoval ondrej.hav (24. 07. 2013 18:13)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
Jestli jdeš v úterý tak se tam potkáme :-) Na co se zaměřit, to je těžký no, hlavně vědět co je P, NP a NPC. Jinak samozřejmě FF můžeš využít jako argument pro ten původní příklad.
Offline
#13 24. 07. 2013 18:17
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Spíš plánuju až ten další měsíc, uvidím jak budu stíhat. Ty P, NP a NPC právě nechápu. :-( Učil ses jen z těch skript, nebo bys doporučil i něco jiného (myslím ohledně těch P, NP, NPC)?
Offline
#14 24. 07. 2013 18:25
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Na pochopení nejlepší ty skripta. Pěkný shrnutí jsou ty materiály z Dropboxu, jestli máš. Jeslti ne, napiš a pošlu.
Offline
#15 24. 07. 2013 20:16
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Z Dropboxu nemám, ale myslim že vim, co myslíš (v podstatě vypracované otázky na cca 20 stránkách). Mě šlo spíš o nějaké jednoduché vyvětlení např. na obrázkách. Nějak jednoduše prostě, jen z těch skript moc chytrej nejsem. když pochopím apson nějakej uvod do těch tříd problémů, tak pak už se to nějak naučim.
Offline
#16 24. 07. 2013 20:29
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
↑ Shelber:
Tak o ničem takovým nevím. Ale napiš, když nebudeš něco vědět a já se pokusím. Nebo někdo jiný tady.
Offline
#17 24. 07. 2013 20:53
Re: Hranový a uzlový stupeň souvislosti grafu
↑ ondrej.hav:
Dobrá, děkuju.
Ještě pro upřesnění, než půjdu na pokročilejší látku:
Věta 4.7 Menger mi udává nějakou definici, která je popsaná výše. Pro mě je ale důležité, že mohu upravou daného grafu přentransformovat graf do formy, která odpovídá typu "Zdroj-Stok" (dle pravidla popsaného v důkazu této věty). Na graf typu "Zroj-Stok" mohu pak jednoduše použít FF algoritmus. Čili jsem ulohu na souvislost grafu převedl z "maticového standardního" řešení do řešení typu "Zdroj-Stok" a jelikož vím, že řešení typu "Zdroj-Stok" spadá do P problémů, tak do něj bude spadat i toto nové řešení.
Nevim jestli to píšu uplně přeně, když tak mě prosím oprav..
Offline
#18 24. 07. 2013 21:30
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Hranový a uzlový stupeň souvislosti grafu
Jop. Asi bych raději než FF napsal Edmonds-Karpův, ale to už je asi jedno. Důležité je to, že si to převedl na tok.
Offline