Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 07. 2013 19:26
Grundyho funkce
Vysvětlili byste mi prosím Grundyho funkci?
Nechápu dvě věci. Za prvé mi už delší dobu není uplně jasné acyklické číslování (vždy jsem čísloval od počátku, tedy od uzly pouze s výstupními hranami až ke konci dle směru šipek hran, ale jak jsem teď zjistil, bude to mít hlubší pravidlo).
A druhá věc - nechápu uplně algoritmus dole (resp bod č. 2). bylo by možné popsat mi přímo funkci algoritmu např. pro tři kroky?
Offline
#2 27. 07. 2013 21:17
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Grundyho funkce
Jak to říkáš, tak je to správně. Pokud jich je více vstupních uzlů můžeš vybrat kterýkoli. Žádně větší záludnost by být neměla.
Grundi: Bereš uzly v sestupném pořadí jejich acyklického číslování. Vždy se podíváš do všech uzlů, do kterých vede hrana a Grundiho funkce bude nejmenší nepoužité číslo.
Takže máš uzel který má 2 následníky. Jejich hodnoty jsou 1 a 2 -> uzel bude mít 0 (nejmenší nepoužité z 0, 1, 2...)
Pokud máš uzel, který má 3 následníky a jejich ohodnocení je 0, 1, 2 -> uzel bude mít hodnotu 3
P.S.: Ve skriptech, která používáš na straně 43 jsou to hodnoty uzlů číslo 4 a 2. :-)
Offline
#3 27. 07. 2013 22:11
Re: Grundyho funkce
↑ ondrej.hav:
Furt to nechápu :-(
Jedu z uzlu 7 a dívám se do uzlů, do kterých z uzlu 7 vede hrana - 1, 2, 5, 6 (mám 4 následníky). Nejmenší nepoužité číslo je 0, takže 7 = 0, ale jak dál?
Offline
#4 27. 07. 2013 22:48 — Editoval ondrej.hav (27. 07. 2013 22:49)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Grundyho funkce
Postupuješ odzadu a ten graf je orientovaný. Takže z uzlu 7 žádné hrany nevedou.
Uzel 7 má automaticky nulu. To je dané.
Jdeš po acyklickém číslování zpět - tedy uzel 6. Z uzlu 6 vede pouze hrana do uzlu 7. Ten má nulu... použiješ jedničku.
Znovu dolů po acyklickém číslování - uzel 5. Z uzlu 5 vedou hrany do 6 a 7, které mají hodnoty 0 a 1 > použiješ dvoujku
Uzel 4 - hrany vedou do uzlů 5 a 6, které mají hodnoty 2 a 1 -> můžeš tedy znovu použít nulu
Uzel 3 - jedna hrana do uzlu 4, který má hodnotu 0 -> použiješ jedničku
Uzel 2 - hrany do 3, 5, 7 s hodnotami 1, 2, 0 -> použiješ 3
Uzel 1 - hrany do 2, 3, 7 s hodnotami 3, 1, 0 -> použiješ 2
Uf... Takhle už dobrý?
Offline
#5 28. 07. 2013 00:45
Re: Grundyho funkce
↑ ondrej.hav:
Už jo, děkuju za rozepsání.
Mám ale problém hned s další látkou - jádro grafu bez lichých cyklů. V kroku "hledání kvazikomponent" nechápu, proč jsou ty komponenty zrovna takto. Chápal bych tu vlevo nahoře, ale ne ty ostatní. Kvazikomponenta je přeci oblast grafu, z níž se už nelze dostat (díky orientaci hran) a nebo naopak lze se dostat pouze ven, ale ne nazpátek.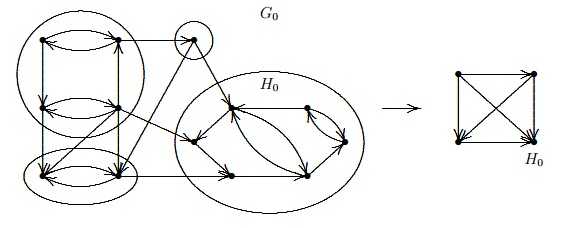
Offline
#6 28. 07. 2013 02:34 — Editoval ondrej.hav (30. 07. 2013 22:12)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Grundyho funkce
↑ Shelber:
Kvazikomponenta je maximální silně souvislý podgraf. Takže musí existovat orientovaná cesta mezi všemi dvojicemi uzlů v kvazikomponentě. Prostě a jednoduše se dostaneš uvnitř kvazikomponenty odkudkoli kamkoli. To co jsi definoval ty není správně.
Podívej se na následující obrázek: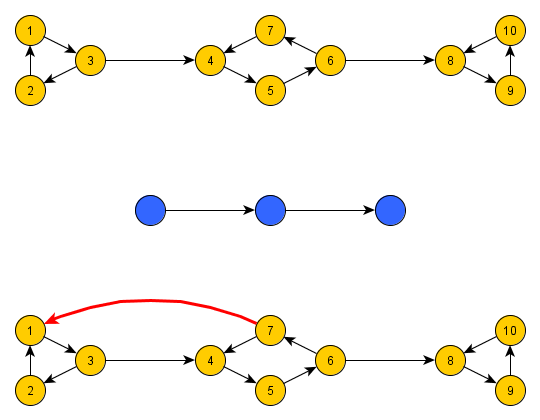
Na prvním obrázku jsou 3 cykly. To jsou jistě kvazikomponenty, protože se dostaneš z každého uzlu do všech ostatních.
Na kondenzaci je vidět, že prostřední uzel kondenzace je vstupní i výstupní.
V tom obrázku dole je zvýrazněna hrana, která zajišťuje, že se dostaneš mezi všemi uzly 1-6. Tudíž pak se ty 2 kk spojí.
Z toho plyne, že z kvazikomponenta může být vstupní i výstupní uzel kondenzace, pokud to není vůči jednomu uzlu kondenzace najedenou.
Doufám, že jsem ti v tom neudělal ještě větší bordel, než si v tom měl.
Offline
#7 28. 07. 2013 11:25
Re: Grundyho funkce
↑ ondrej.hav:
Takže ten spodní obrázek by tím pádem měl jen dvě kvazikomponenty?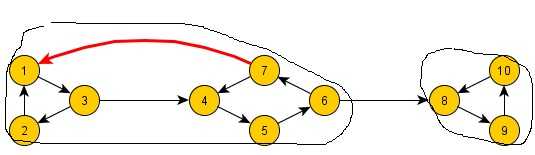
Offline
#9 28. 07. 2013 14:11
Re: Grundyho funkce
↑ ondrej.hav:
Mohl bys mi prosím objasnit celé řešení příkladu? Určím kvazikomponenty, sestavím kondenzaci a pak vyberu prvek v kondenzaci, do kterého směřují všechny šipky (výstupní). Ten si samostatně rozkreslím a zvolím v něm libovolný bod x. Z toho bodu jedu a hledám sudý sled (v podstatě ob jeden bod dle směru šipek). Ok, tohle chápu. Ale u toho grafu G1 se ztrácím. To už přeci není samostatná kvazikomponenta.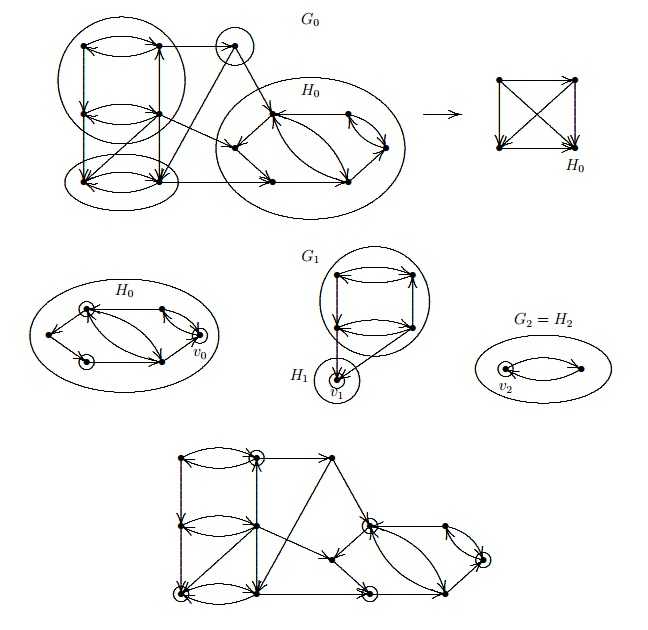
Offline
#10 28. 07. 2013 14:35
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Grundyho funkce
↑ Shelber:
Algoritmus je důkazem věty: Každý orientovaný graf bez cyklů liché délky má jádro.
A důkaz říká: Vezmi výstupní komponentu 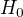 a v ní sestroj množinu
a v ní sestroj množinu 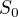 To jsi popsal správně jako takové uzly do nichž vede z náhodně vybraného uzlu sled sudé délky.
To jsi popsal správně jako takové uzly do nichž vede z náhodně vybraného uzlu sled sudé délky.
Pokud by byl 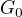 silně souvislý, tak by algoritmus zkončil.
silně souvislý, tak by algoritmus zkončil.
Pokud 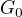 není silně souvislý (má více kvazikomponent), je dalším krokem algoritmu sestavit nový graf
není silně souvislý (má více kvazikomponent), je dalším krokem algoritmu sestavit nový graf .
.
A ten se sestaví tak, že z původního grafu vyjmeš celou množinu 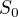 a všechny uzly, ze kterých vede do
a všechny uzly, ze kterých vede do 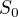 hrana.
hrana.
A celý postup znovu opakuješ od začátku.
Offline