Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 08. 2013 23:14
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
linearizace rovnic a dál
Téma pro mě není jednoduché a bylo mi už mírně vysvětleno, je to trochu test na zdejší komunitu. Vezměme příklad:
u_{x}.u+u_{y}.u+u_{z}.u=0
a linearizujme podle proměnné u, (indexy jsou parciální derivace).
U_{x}.u+U_{y}.u+U_{z}.u+u_{x}.U+u_{y}.U+u_{z}.U=0
kde velkým písmenem je teď neznámá proměnná a s malým písmenem pak určitá konstantní hodnota. Tento postup jde obecně vysvětlit asi takto:
platí : rovnice (s u)=0
platí ta samá rovnice s perturbací U a konstantou u
rovnice(U+u)=0
teď obě rovnice odečti a vyjde ti linearizovaná forma rovnic.
(nejspíš) Totéž by mělo vycházet poměrně komplikovaným postupem, který mám někde napsaný na linearizaci operátoru.
Zajímalo by mě, jestli nejde jít do dalšího řádu v poruše a jak se to provádí- a případně jaký typ rovnic by pak vycházel (já osobně jsem vycházel z intuitivního použití Taylora rozvoje ne na funkci ale na rovnici)- jestli by vůbec byly nějak řešitelné... Případně jen jestli jste někdo/někdy na něco podobného narazili.
Ještě dodám, že já to matematicky nepotřebuju a konkrétně jsem na to narazil při linearizaci (často zjedodušených) Eulerových rovnic. Vycházeli pak rovnice pro různé vlny v atmosféře. Omlouvám se za případné nepřesnosti, které se patrně vyskytly. Matematiku asi dost znásilňuju.
Offline
#3 06. 08. 2013 16:14
Re: linearizace rovnic a dál
↑ grizzlybear:
Omlouvám se, ale asi jsem nepochopil tvůj problém. Dovolím si tedy zrekapitulovat, jak jsem pochopil linearizaci tvé parciální diferenciální rovnice (a taky si to při tom porovnám v hlavě):
Máš rovnici:
Součin funkce a derivece si nahradíš linearizací (např. pro x):
(velkými písmenky konstanty - někde se mi vytratila konstanta, která by vznilka při linearizaci diferenciálem a posléze by "zlobila" na pravé straně. Předpokládám tedy, že lze z nějakých spíše fyzikálních důvodů zanedbat)
Tím se vlastně dostaneš na parciální diferenciální rovnici:
Tedy po drobné algebraické úpravě:
Protože (i) pro parciální diferenciální rovnice platí, že je-li u řešením, je řešením i Ku, můžeš si položit K=1.
Z toho tedy vyjde lineární parciální diferenciální rovnice:
_____________________________
Tedy vlastě jsi linearizoval kvazilineární rovnici. Tady v tom případě má pravdu Rumburak, že metoda "kouknu a vidím" je lepší. Spíš mám pocit, že by mohl tenhle postup linearizace, tedy náhrada:
, fungovat na větší třídu kvazilineárních rovnic.
______________________________
A ke tvé otázce, zda by mělo smysl rozvádět do vyšších řádů - velmi pravděpodobně ne. Tím by se ti totiž objevily derivace pod mocninou a jestli je to u obyčejných diferenciálních rovnic dosti nepříjemné, bude do u parciálních celkem na houby. Přitom hlavním smyslem linearizace je studovaný systém aproximovat systémem, který je lépe řešitelný.
Доктор сказал «в морг» — значит в морг!
Offline
#5 06. 08. 2013 16:51
Re: linearizace rovnic a dál
↑ Brano:
Nemá společného nic:-( Prostě jsem si jen vybavil, že tohle "vyhánění konstanty" je celkem snadné a napsal jsem první blbost, která mě napadla. Konkrétně zde by ten správný důvod měl znít - a teď už snad nestřelím pudla - že jde rovnici transformovat do souřadnic y_i = Kx_i, čím se K objeví i jako prvek násobící parciální derivace a bude možné obě rovnice podělit K. Pak se jen přeznačí souřadnice.
Доктор сказал «в морг» — значит в морг!
Offline
#6 06. 08. 2013 20:48
Re: linearizace rovnic a dál
↑ Formol:
tak je to dobre :-)
inak aj ja sa priklanam k Rumburakovi, ze linearizovat ju je zbytocne.
↑ grizzlybear: ake mas presne zadanie? je tam povedane: "linearizujte ..." ?
Offline
#7 08. 08. 2013 17:25
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: linearizace rovnic a dál
↑ Rumburak:
Nestačilo, ale to, co říkáš je patrně správně. To, co uvádím v příkladu není zas tak podstatné, můžeš si vymyslet vlastní rovnici a tu linearizovat. Příklad je něco jako u.div \vec{v}=0. O řešení linearizované rovnice jako takové mi taky tolik nejde- většinou dosazuju "vlnu" exp(ik(x-ct)). k=\frac{2\pi}{\lambda}. c- je rychlost šíření, může být komplexní. Ale to odbočuju.
Offline
#8 08. 08. 2013 17:44 Příspěvek uživatele grizzlybear byl skryt uživatelem grizzlybear. Důvod: tex není správně napsán
#9 08. 08. 2013 17:49
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: linearizace rovnic a dál
↑ Brano:
Zadání dost upravuju, neb se v tom vrtám- úloha není z žádný učebnice. To "jednodušší" je linearizujte (nějakou) rovnici. To složitější je jděte dál v rozvoji (jestli to vůbec jde).
Prakticky to, co jsem udal za příklad je nedobře napsaná rovnice kontinuity:
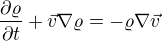
Offline
#10 08. 08. 2013 18:23
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: linearizace rovnic a dál
↑ grizzlybear:
to co jsem zapomněl a je dost podstatné vyškrtneme (položíme rovné nule) kvadratické členy u perturbací. Druhak "konstantě" u se v jedné učebnici říká základní stav.
základní stav: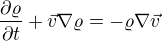
stav s perturbací: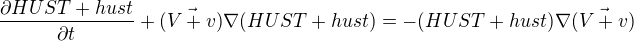
nechce se mi to vypisovat všechno, ale třeba druhý člen na levé straně je:
člen:
je zanedbán, poslední člen zmízí z odečítání základního stavu a zůstanou lineární členy.
Můj přístup byl takový mlhavý a díky "kvadratickým členům" (nejsem si jistý správnou terminologií) by se dal označit jako "derivace součinu".
Ale lépe řečeno jsem používal parciální derivaci a pak nahrazení danou veličinou. (je to vyloženě pseudopostup) a na jiné rovnice nejspíš nefunguje. Tj. derivuj rovnici podle hustoty a nahraď to HUSTOTOU. Tj. pro jediný člen: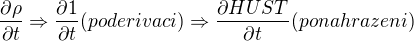
Jsem toho názoru, že tyhle dva postupy dávají pro nějaké rovnice totéž. Jinak díky za názory. Vyjadřovat se k těmto otázkám v tomhle teple je úctyhodné. :)
Offline